题目内容
若函数f（x）=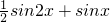
，则f′（x）是
- A.仅有最小值的奇函数
- B.仅有最大值的偶函数
- C.既有最大值又有最小值的偶函数
- D.非奇非偶函数
C
分析：先求导，转化为二次函数型的函数并利用三角函数的单调性求其最值，再利用函数的奇偶性的定义进行判断其奇偶性即可．
解答：∵函数f（x）=，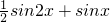
∴f′（x）=cos2x+cosx=2cos2x+cosx-1=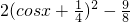
，当cosx=
时，f′（x）取得最小值
；当cosx=1时，f′（x）取得最大值2．
且f′（-x）=f′（x）．即f′（x）是既有最大值，又有最小值的偶函数．
故选C．
点评：熟练掌握复合函数的导数、二次函数型的函数的最值、三角函数的单调性及函数的奇偶性是解题的关键．
分析：先求导，转化为二次函数型的函数并利用三角函数的单调性求其最值，再利用函数的奇偶性的定义进行判断其奇偶性即可．
解答：∵函数f（x）=
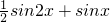，∴f′（x）=cos2x+cosx=2cos2x+cosx-1=
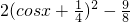，当cosx=时，f′（x）取得最小值；当cosx=1时，f′（x）取得最大值2．且f′（-x）=f′（x）．即f′（x）是既有最大值，又有最小值的偶函数．
故选C．
点评：熟练掌握复合函数的导数、二次函数型的函数的最值、三角函数的单调性及函数的奇偶性是解题的关键．
练习册系列答案
相关题目
若函数f（x）=sin2x，则f′（
）的值为（ ）
| π |
| 6 |
A、
| ||
| B、0 | ||
| C、1 | ||
D、-
|