题目内容
如图,在棱长为1的正方体ABCD—A1B1C1D1中,点E是棱BC的中点,点F是棱CD上的动点.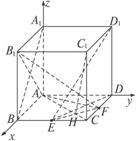
(1)试确定点F的位置,使得D1E⊥平面AB1F;
(2)当D1E⊥平面AB1F时,求二面角C1—EF—A的大小.(结果用反三角函数值表示)
解:以A为坐标原点,建立如图所示的空间直角坐标系.

(1)设DF=x,则A(0,0,0),B(1,0,0),D(0,1,0),A1(0,0,1),B1(1,0,1),D1(0,1,1),E(1,![]() ,0),F(x,1,0).
,0),F(x,1,0).
所以![]() =(1,-
=(1,-![]() ,-1),
,-1),![]() =(1,0,1),
=(1,0,1),![]() =(x,1,0).
=(x,1,0).
所以![]() ·
·![]() =1-1=0,即D1E⊥AB1.
=1-1=0,即D1E⊥AB1.
于是D1E⊥平面AB1F?D1E⊥AF![]()
![]() ·
·![]() =0
=0![]() x-
x-![]() =0,即x=
=0,即x=![]() .
.
故当点F是CD的中点时,D1E⊥平面AB1F.
(2)当D1E⊥平面AB1F时,F是CD的中点.
又E是BC的中点,连结EF,则EF∥BD.
连结AC,设AC与EF交于点H,则AH⊥EF.
连结C1H,则CH是C1H在底面ABCD内的射影.
所以C1H⊥EF,即∠AHC1是二面角C1—EF—A的平面角.
因为C1(1,1,1),H(![]() ,
,![]() ,0),
,0),
所以![]() =(
=(![]() ,
,![]() ,1),
,1),![]() =(-
=(-![]() ,-
,-![]() ,0).
,0).
所以cos∠AHC1= =
=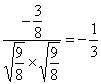 ,
,
即∠AHC1=arccos(-![]() )=π-arccos
)=π-arccos![]() .
.
故二面角C1—EF—A的大小为π-arccos![]() .
.
点拨:用向量法求二面角的大小时,应结合具体图形来判断求出的是二面角的平面角,还是它的补角.

练习册系列答案
相关题目
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
