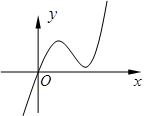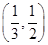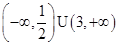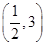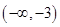题目内容
定义在R上的可导函数f(x),已知y=e f ′(x)的图象如下图所示,则y=f(x)的增区间是
| A.(-∞,1) | B.(-∞,2) | C.(0,1) | D.(1,2) |
B
解析试题分析:若f‘(x)≥0,则e f ′(x)≥ e0=1,由图知当x<2时,e f ′(x)≥ 1,所以y=f(x)的增区间是(-∞,2) 。
考点:指数函数的图像;指数函数的性质;利用导数研究函数的单调性。
点评:要求函数y=f(x)的增区间,只需求f‘(x)>0的解集。因此根据y=e f ′(x)的图像判断f‘(x)>0的解集时解题的关键。属于中档题。

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
设连续函数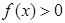 ,则当
,则当 时,定积分
时,定积分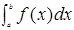 的符号
的符号
| A.一定是正的 |
| B.一定是负的 |
C.当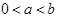 时是正的,当 时是正的,当 时是负的 时是负的 |
| D.以上结论都不对 |
已知 ,若
,若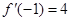 ,则
,则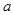 的值等于( )
的值等于( )
A. | B. | C. | D. |
已知二次函数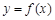 的图象如图所示,则它与
的图象如图所示,则它与 轴所围图形的面积为:
轴所围图形的面积为:
A.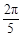 | B. | C.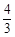 | D. |
若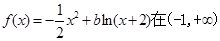 上是减函数,则
上是减函数,则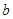 的取值范围是( )
的取值范围是( )
A.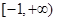 | B.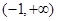 | C.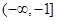 | D.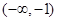 |
曲线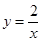 与直线
与直线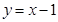 及
及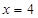 所围成的封闭图形的面积为( )
所围成的封闭图形的面积为( )
A.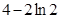 | B.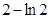 |
C.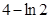 | D.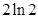 |
直线y=x与抛物线 y=x(x+2)所围成的封闭图形的面积等于
y=x(x+2)所围成的封闭图形的面积等于
A. | B. | C.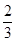 | D. |
已知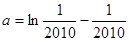 ,
, ,
,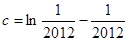 则( )
则( )
A.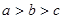 | B.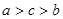 | C. | D.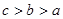 |
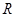 上的函数
上的函数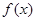 满足
满足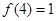 ,
,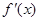 为
为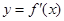 的图象如图所示.若两正数
的图象如图所示.若两正数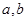 满足
满足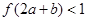 ,则
,则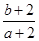 的取值范围是( )
的取值范围是( )