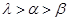题目内容
直线y=x与抛物线 y=x(x+2)所围成的封闭图形的面积等于
y=x(x+2)所围成的封闭图形的面积等于
A.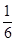 | B.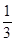 | C.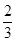 | D. |
A
解析试题分析:先联立方程,组成方程组,求得交点坐标,可得被积区间,再用定积分表示出曲线y=x2+2x与直线y=x所围成的封闭图形的面积,即可求得结论.y=x与y=x(x+2)联立方程组得到x=-1,y=-1,或x=0,y=0,那可可知直线y=x与抛物线 y=x(x+2)所围成的封闭图形的面积等于
y=x(x+2)所围成的封闭图形的面积等于
S=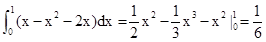 ,故选A
,故选A
考点:本题主要考查了定积分的几何意义的运用,求解曲边梯形的面积。
点评:解决该试题的关键是利用定积分求面积,确定被积区间及被积函数,以及被积函数的原函数的问题,进而得到求解。

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 =( )
=( )
A. | B.2 | C. | D. |
定义在R上的可导函数f(x),已知y=e f ′(x)的图象如下图所示,则y=f(x)的增区间是
| A.(-∞,1) | B.(-∞,2) | C.(0,1) | D.(1,2) |
已知 ,则( )
,则( )
A. | B. | C. | D.以上都有可能 |
函数f(x)=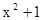 在(1,2)处的切线斜率为( )
在(1,2)处的切线斜率为( )
| A.1 | B.2 | C.3 | D.4 |
函数 图象如图,则函数
图象如图,则函数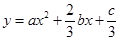 的单调递增区间为( )
的单调递增区间为( )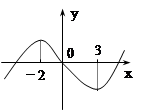
A.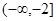 | B.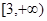 | C.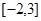 | D. |
已知函数 有两个零点
有两个零点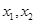 ,则( )
,则( )
A.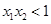 | B.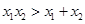 | C.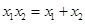 | D.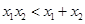 |
设点 在曲线
在曲线 上,点
上,点 在曲线
在曲线 上,则
上,则 最小值为 ( )
最小值为 ( )
A. | B. | C. | D. |
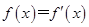 的较大实数根叫做函数
的较大实数根叫做函数 的“轻松点”,若函数
的“轻松点”,若函数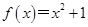 ,
,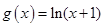 ,
,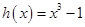 的“轻松点”分别为
的“轻松点”分别为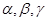 ,则
,则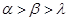 B.
B.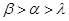 C.
C. D.
D.