题目内容
正四面体S—ABC中,E为SA的中点,F为 的中心,则直线EF与平面ABC所成的角的正切值是 。
的中心,则直线EF与平面ABC所成的角的正切值是 。
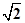
解析试题分析:连接SF,则SF⊥平面ABC.连接AF并延长交BC于H,取线段AF的中点G,连接EG,由E为SA的中点,则EG∥SF,∴EG⊥平面ABC,∴∠EFG即为EF与平面ABC所成的角.
设正四面体的边长为a,则AH=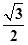 a,且AF=
a,且AF=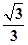 a,
a,
在Rt△AGE中,AE=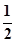 a,AG=
a,AG=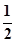 AF=
AF=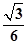 a,∠EGA=90°,
a,∠EGA=90°,
∴EG=AE2-AG2=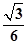 a.在Rt△EGF中,FG=
a.在Rt△EGF中,FG=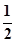 AF=
AF=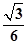 a,EG=
a,EG=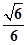 a,∠EGF=90°,
a,∠EGF=90°,
∴tan∠EFG=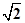
即EF与平面ABC所成的角的正切值是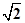 。
。
考点:本题主要考查立体几何中几何体的特征,角的计算。
点评:基础题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,本题中先做出线面角,再证出线面角,最后把角放到一个三角形中解出结果。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 和直线
和直线 ,给出下列条件:①
,给出下列条件:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .则使
.则使 成立的充分条件是 .(填序号)
成立的充分条件是 .(填序号) 是两个不同的平面,
是两个不同的平面, 是两条不同直线.①若
是两条不同直线.①若 ,则
,则
 ,则
,则
 ,则
,则
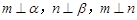 ,则
,则 以上命题正确的是 .(将正确命题的序号全部填上)
以上命题正确的是 .(将正确命题的序号全部填上) 的底面是边长为1的正方形,侧棱长
的底面是边长为1的正方形,侧棱长 ,则异面直线
,则异面直线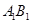 与
与 的夹角大小等于___________.
的夹角大小等于___________.
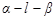 的大小是60°线段
的大小是60°线段 所成的角
所成的角 与平面
与平面 所成的角的正弦值是___________.
所成的角的正弦值是___________.