题目内容
1.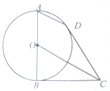 如图所示,AB为圆O的直径,BC为圆O的切线,B为切点,D为圆O上一点,AD∥OC.
如图所示,AB为圆O的直径,BC为圆O的切线,B为切点,D为圆O上一点,AD∥OC.(Ⅰ)求证:OC平分∠BCD;
(Ⅱ)若AD•OC=8,求圆O半径R的值.
分析 (Ⅰ)连接BD,OD,证明△OBC≌△ODC,可得OC平分∠BCD;
(Ⅱ)证明△BAD∽△COD,利用AD•OC=8,即可求圆O半径R的值.
解答 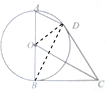 (Ⅰ)证明:连接BD,OD,
(Ⅰ)证明:连接BD,OD,
∵CB是圆O的切线,∴∠ABC=90°,
∴∠BOC=∠A,∠DOC=∠ODA,…(2分)
∵OA=OD,
∴∠A=∠ODA,
∴∠BOC=∠DOC,
∵OB=OD,OC=OC,…(4分)
∴△OBC≌△ODC,
∴OC平分∠BCD.…(5分)
(Ⅱ)解:∵AO=OD,
∴∠DAO=∠DOC,
∵AB是直径,
∴∠OBC=∠ADB=90°.…(7分)
∴△BAD∽△COD,
∴AD•OC=AB•OD=8=2R2.…(9分)
∴R=2. …(10分)
点评 本题考查相似三角形的判断,考查学生分析解决问题的能力,正确判断三角形相似是关键.

练习册系列答案
相关题目
9.正方体的内切球和外接球的表面积之比为( )
| A. | 3:1 | B. | 3:4 | C. | 4:3 | D. | 1:3 |
16.已知集合A={x|-1≤x≤1},B={x|0≤x≤2},则A∩B=( )
| A. | [-1,0) | B. | [-1,0] | C. | [0,1] | D. | (-∞,1)∪[2,+∞) |
12.设等差数列{an}的前n项和为Sn,且满足S19>0,S20<0,则$\frac{{S}_{1}}{{a}_{1}}$,$\frac{{S}_{2}}{{a}_{2}}$,$\frac{{S}_{3}}{{a}_{3}}$,…,$\frac{{S}_{19}}{{a}_{19}}$中最大项为( )
| A. | $\frac{{S}_{8}}{{a}_{8}}$ | B. | $\frac{{S}_{9}}{{a}_{9}}$ | C. | $\frac{{S}_{10}}{{a}_{10}}$ | D. | $\frac{{S}_{11}}{{a}_{11}}$ |
8.设tanα、tanβ是方程x2-3x+2=0的两个根,则tan(α+β)=( )
| A. | -3 | B. | 3 | C. | -1 | D. | 1 |
 已知△ABC中,AB=AC,D为△ABC外接圆劣弧$\widehat{AC}$上的点(不与点A,C重合),延长BD至E,延长AD交BC的延长线于F
已知△ABC中,AB=AC,D为△ABC外接圆劣弧$\widehat{AC}$上的点(不与点A,C重合),延长BD至E,延长AD交BC的延长线于F