题目内容
设双曲线C: 与直线l:x+y=1相交于两个不同的点A、B,
与直线l:x+y=1相交于两个不同的点A、B,
(Ⅰ)求双曲线C的离心率e的取值范围:
(Ⅱ)设直线l与y轴的交点为P,且 ,求a的值。
,求a的值。
 与直线l:x+y=1相交于两个不同的点A、B,
与直线l:x+y=1相交于两个不同的点A、B,(Ⅰ)求双曲线C的离心率e的取值范围:
(Ⅱ)设直线l与y轴的交点为P,且
 ,求a的值。
,求a的值。解:(Ⅰ)由C与l相交于两个不同的点,故知方程组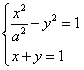 有两个不同的实数解,
有两个不同的实数解,
消去y并整理得(1-a2)x2+2a2x-2a2=0, ①
所以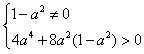 ,解得
,解得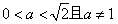 ,
,
双曲线的离心率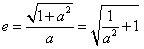 ,
,
∵ ,
,
∴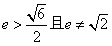 ,
,
即离心率e的取值范围是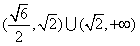 。
。
(Ⅱ)设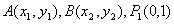 ,
,
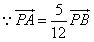 ,
,
∴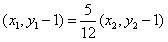 ,由此得
,由此得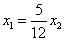 ,
,
由于x1,x2都是方程①的根,且1-a2≠0,
所以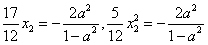 ,
,
消去x2,得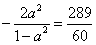 ,
,
由a>0,所以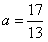 。
。
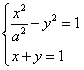 有两个不同的实数解,
有两个不同的实数解,消去y并整理得(1-a2)x2+2a2x-2a2=0, ①
所以
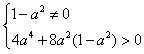 ,解得
,解得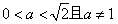 ,
,双曲线的离心率
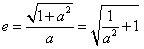 ,
,∵
 ,
,∴
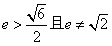 ,
,即离心率e的取值范围是
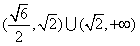 。
。(Ⅱ)设
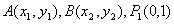 ,
,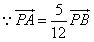 ,
, ∴
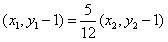 ,由此得
,由此得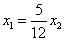 ,
,由于x1,x2都是方程①的根,且1-a2≠0,
所以
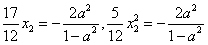 ,
,消去x2,得
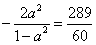 ,
,由a>0,所以
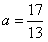 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 设双曲线C:
设双曲线C: 与直线l:x + y = 1相交于两个不同的点A、B
与直线l:x + y = 1相交于两个不同的点A、B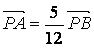 ,求
,求 的值
的值