题目内容
16.若x∈R,则函数f(x)=3-5sinx-cos2x的最小值为-2.分析 根据f(x)=sin2x-5sinx+2=${(sinx-\frac{5}{2})}^{2}$-$\frac{17}{4}$,再利用二次函数的性质求得它的最值.
解答 解:函数f(x)=3-5sinx-cos2x=sin2x-5sinx+2=${(sinx-\frac{5}{2})}^{2}$-$\frac{17}{4}$,
故当sinx=1时,函数f(x)取得最小值为-2;当sinx=-1时,函数f(x)取得最大值为 8,
故答案为:-2.
点评 本题主要考查同角三角函数的基本关系,二次函数的性质,属于基础题.

练习册系列答案
相关题目
6.已知命题甲为:x>0;命题乙为x2>0,那么( )
| A. | 甲是乙的充要条件 | B. | 甲是乙的充分非必要条件 | ||
| C. | 甲是乙的必要不充分条件 | D. | 甲是乙的既不充分也不必要条件 |
8.若$\overrightarrow{OA}$=3e1,$\overrightarrow{OB}$=7e2,$\overrightarrow{PB}$=4$\overrightarrow{AP}$,$\overrightarrow{OP}$=me1+ne2,则m-n等于( )
| A. | $\frac{1}{4}$ | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
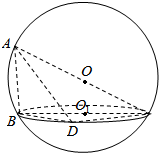 如图所示,AC为球O的直径,BC是截面圆O1的直径,点D在圆O1上,根据球的截面性质:球心和截面圆心的连线垂直于截面,求证:
如图所示,AC为球O的直径,BC是截面圆O1的直径,点D在圆O1上,根据球的截面性质:球心和截面圆心的连线垂直于截面,求证: