题目内容
(13分)设函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 在
在![]() 内没有极值点,求
内没有极值点,求![]() 的取值范围;
的取值范围;
解析:(1)![]()
又![]() ,
,![]() 当
当![]() 或
或![]() 时,
时,![]()
当![]() 时,
时,![]()
![]() 函数
函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() (4分)
(4分)
(2)由题设可知,方程![]() 在
在![]() 上没有实根
上没有实根
![]()
![]() ,解得
,解得![]() (8分)
(8分)
(3)![]()
![]() ,
,![]() 由(1)知
由(1)知![]() ≤
≤![]()
又![]()
![]()
![]()
而![]()
![]()
![]() (10分)
(10分)
又![]() ≤
≤![]() 在
在![]() 上恒成立
上恒成立
![]()
![]() ≤
≤![]() 即
即![]() ≤
≤![]()
即![]() ≤
≤![]() ,在
,在![]() 上恒成立
上恒成立
![]()
![]() 的最小值为
的最小值为![]()

练习册系列答案
相关题目
 对任意的实数
对任意的实数 ,都有
,都有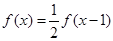 ,且当
,且当 时,
时, 。
。 时,求
时,求 ,试问:在它的图象上是否存在点
,试问:在它的图象上是否存在点 ,使得函数在点
,使得函数在点 平行。若存在,那么这样的点
平行。若存在,那么这样的点 ,且
,且  ,记
,记 ,求证:
,求证:  。
。 ,已知
,已知 ,且
,且 ,曲线
,曲线 在x=1处取极值.
在x=1处取极值. 的递增区间为
的递增区间为 ,求
,求 的取值范围;
的取值范围;
 是与
是与 无关的常数
无关的常数 时,恒有
时,恒有 ,求实数
,求实数 的最小值
的最小值