题目内容
f(x)的定义域为R,且f(x)=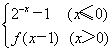 ,若方程f(x)=x+a有两不同实根,则a的取值范围为
,若方程f(x)=x+a有两不同实根,则a的取值范围为
A.(-∞,1) B.(-∞,1] C.(0,1) D.(-∞,+∞)
A

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
f(x)的定义域为R,且f(x)=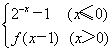 ,若方程f(x)=x+a有两不同实根,则a的取值范围为
,若方程f(x)=x+a有两不同实根,则a的取值范围为
A.(-∞,1) B.(-∞,1] C.(0,1) D.(-∞,+∞)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案