题目内容
(本小题12分)为丰富高三学生的课余生活,提升班级的凝聚力,某校高三年级6个班(含甲、乙)举行唱歌比赛.比赛通过随机抽签方式决定出场顺序.
求:(1)甲、乙两班恰好在前两位出场的概率;
(2)比赛中甲、乙两班之间的班级数记为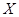 ,求
,求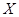 的分布列和数学期望.
的分布列和数学期望.
【答案】
(1)甲、乙两班恰好在前两位出场的概率为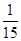 ;(2)分布列:
;(2)分布列:
|
|
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
随机变量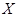 的数学期望为
的数学期望为
【解析】(1)设“甲、乙两班恰好在前两位出场”为事件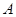 ,则
,则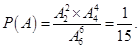
(2)先确定随机变量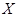 的可能取值为
的可能取值为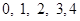 .然后求出每个值对应的概率。列出分布列根据期望公式求解即可。
.然后求出每个值对应的概率。列出分布列根据期望公式求解即可。
解:(1)设“甲、乙两班恰好在前两位出场”为事件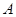 ,则
,则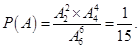
所以 甲、乙两班恰好在前两位出场的概率为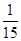 ………………………………4分
………………………………4分
(2)随机变量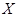 的可能取值为
的可能取值为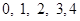 .
.
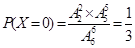 ,
, 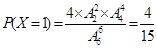 ,
, 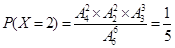 ,
,
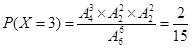
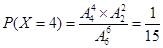 ……………………10分
……………………10分
随机变量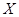 的分布列为:
的分布列为:
|
|
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
因此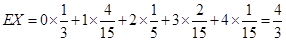 ,
,
即随机变量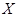 的数学期望为
的数学期望为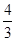 .
…………………………12分
.
…………………………12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(本小题12分)为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算电费。每月用电不超过100度时,按每度0.57元计算,每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.5元计算。(1)设月用电x度时,应交电费y元,写出y关于x的函数关系式;(2)小明家第一季度缴纳电费情况如下:
| 月份 | 一月 | 二月 | 三月 | 合计 |
| 交费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
问小明家第一季度共用电多少度?
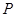
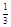
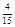
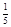
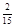
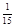
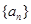 为等差数列
为等差数列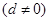 ,
,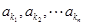 恰为等比数列,且
恰为等比数列,且 ,求
,求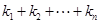 。
。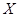 ,求
,求