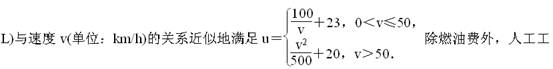题目内容
(本题满分15分)等比数列{![]() }的前n项和为
}的前n项和为![]() , 已知对任意的
, 已知对任意的![]() ,点
,点![]() ,均在函数
,均在函数![]() 且
且![]() 均为常数)的图像上.
均为常数)的图像上.
(1)求r的值;
(11)当b=2时,记 ![]() 证明:
证明:
对任意的![]() ,不等式
,不等式![]() 成立
成立
(本题满分15分)
解: (1)因为对任意的![]() ,点
,点![]() 均在
均在![]() 的图像上. 所以得
的图像上. 所以得![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
又因为{![]() }为等比数列,所以
}为等比数列,所以![]() ,公比为
,公比为![]() ,
,![]() …………6分
…………6分
(2)当b=2时,![]() ,
,
![]() …………8分
…………8分
则![]() ,所以
,所以![]() …………9分
…………9分
下面用数学归纳法证明![]() 成立.
成立.
① 当![]() 时,左边=
时,左边=![]() ,右边=
,右边=![]() ,因为
,因为![]() ,所以不等式成立. …………10分
,所以不等式成立. …………10分
② 假设当![]() 时不等式成立,
时不等式成立,
即![]() 成立.
成立.
则当![]() 时,
时,
左边=![]()
![]()
所以当![]() 时,不等式也成立. …………14分
时,不等式也成立. …………14分
由①、②可得不等式恒成立. …………15分
【命题立意】:本题主要考查了等比数列的定义,通项公式,以及已知![]() 求
求![]() 的基本题型,并运用数学归纳法证明与自然数有关的命题,以及放缩法证明不等式.
的基本题型,并运用数学归纳法证明与自然数有关的命题,以及放缩法证明不等式.

练习册系列答案
相关题目
 的前四项和
的前四项和 ,且
,且 成等比.
成等比. 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.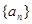 中,
中,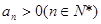 ,公比
,公比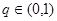 ,且
,且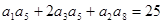 ,
,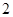 是
是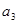 与
与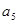 的等比中项。设
的等比中项。设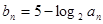 .
.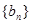 的通项公式;
的通项公式;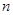 项和为
项和为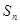 ,
,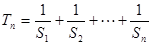 ,求
,求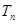 .
.  的前四项和
的前四项和 ,且
,且 成等比.
成等比. 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 恒成立,求实数
恒成立,求实数 的最小值.
的最小值. ,其焦点为F,P(
,其焦点为F,P(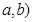 (
( 为直线
为直线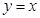 与抛物线M的一个交点,
与抛物线M的一个交点,
 与抛物线交于A,B两点,试问在抛物线M的准线上是否存在一点Q,使得
与抛物线交于A,B两点,试问在抛物线M的准线上是否存在一点Q,使得 QAB为等边三角形,若存在求出Q点的坐标,若不存在请说明理由.
QAB为等边三角形,若存在求出Q点的坐标,若不存在请说明理由.