题目内容
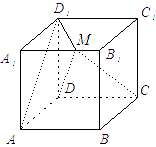(本小题满分12分)
如图, 正方体ABCD－A1B1C1D1的棱长为6, 动点M在棱A1B1上. (1) 当M为A1B1的中点时, 求CM与平面DC1所成角的正弦值;
(2) 当A1M＝
A1B1时, 求点C到平面D1DM的距离.
(Ⅰ) 
(Ⅱ) 
解析:
(1) 
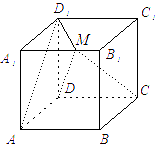在平面A1C1内过点M作MN∥B1C1, 交D1C1于N,
则MN⊥平面DC1, 连NC.
则∠MCN为CM与平面DC1所成角 …………6分
∵MN=B1C1=6, MC=
=9
∴sin∠MCN=
=, 即所求正弦值为.……8分
(2) 连C1M, 作C1H⊥D1M于点H, ∵DD1⊥平面A1C1 ∴D1D⊥C1H
∴C1H⊥平面D1DM, C1H为C1到平面D1DM的距离
又CC1∥D1D，D1D
平面D1DM，∴CC1∥面D1DM，则C到平面D1DM的距离为C1H
∵
C1H·D1M=S△
=18, 而D1M=
=
∴C1H= ∴C到平面D1DM的距离为…………………………………………12分
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
