题目内容
已知数列{an}的前n项和为Sn,且满足an+Sn=2.
(1)求数列{an}的通项公式;
(2)求证数列{an}中不存在任意三项按原来顺序成等差数列;
(3)若从数列{an}中依次抽取一个无限多项的等比数列,使它的所有项和S满足 ,这样的等比数列有多少个?
,这样的等比数列有多少个?
(1)求数列{an}的通项公式;
(2)求证数列{an}中不存在任意三项按原来顺序成等差数列;
(3)若从数列{an}中依次抽取一个无限多项的等比数列,使它的所有项和S满足
 ,这样的等比数列有多少个?
,这样的等比数列有多少个?解:(1)当n=1时,a1+S1=2a1=2,则a1=1.
又an+Sn=2,
∴an+1+Sn+1=2,两式相减得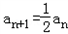 ,
,
∴{an}是首项为1,公比为 的等比数列
的等比数列
∴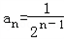
(2)反证法:假设存在三项按原来顺序成等差数列,记为ap+1,aq+1,ar+1(p<q<r)
则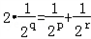 ,∴2●2r﹣q=2r﹣p+1(*)
,∴2●2r﹣q=2r﹣p+1(*)
又∵p<q<r
∴r﹣q,r﹣p∈N*
∴*式左边是偶数,右边是奇数,等式不成立
∴假设不成立原命题得证.
(3)设抽取的等比数列首项为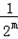 ,公比为
,公比为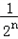 ,项数为k,
,项数为k,
且满足m,n,k∈N,m≥0,n≥1,k≥1,
则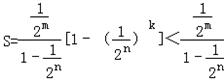
又∵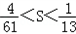
∴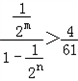
整理得: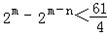 ①
①
∵n≥1 ∴2m﹣n≤2m﹣1.
∴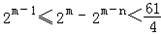
∴m≥4
∵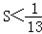 ∴
∴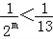
∴m≥4
∴m=4将m=4代入①式整理得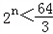 ∴n≥4
∴n≥4
经验证得n=1,2不满足题意,n=3,4满足题意.
综上可得满足题意的等比数列有两个.
又an+Sn=2,
∴an+1+Sn+1=2,两式相减得
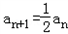 ,
,∴{an}是首项为1,公比为
 的等比数列
的等比数列∴
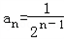
(2)反证法:假设存在三项按原来顺序成等差数列,记为ap+1,aq+1,ar+1(p<q<r)
则
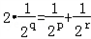 ,∴2●2r﹣q=2r﹣p+1(*)
,∴2●2r﹣q=2r﹣p+1(*)又∵p<q<r
∴r﹣q,r﹣p∈N*
∴*式左边是偶数,右边是奇数,等式不成立
∴假设不成立原命题得证.
(3)设抽取的等比数列首项为
 ,公比为
,公比为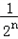 ,项数为k,
,项数为k,且满足m,n,k∈N,m≥0,n≥1,k≥1,
则
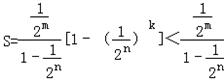
又∵
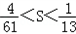
∴
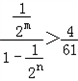
整理得:
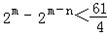 ①
①∵n≥1 ∴2m﹣n≤2m﹣1.
∴
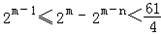
∴m≥4
∵
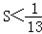 ∴
∴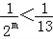
∴m≥4
∴m=4将m=4代入①式整理得
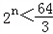 ∴n≥4
∴n≥4经验证得n=1,2不满足题意,n=3,4满足题意.
综上可得满足题意的等比数列有两个.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |