题目内容
14．如图所示，表示阴影部分的二元一次不等式组是（ ）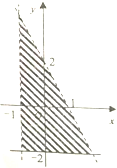
| A． | $\left\{\begin{array}{l}{x+1＞0}\\{2x+y＜2}\\{y≥-2}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+1≥0}\\{2x+y≤2}\\{y＞-2}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{x+1≥0}\\{2x+y＜2}\\{y＞-2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+1＜0}\\{2x+y＜2}\\{y＞-2}\end{array}\right.$ |
分析 由图可知阴影部分在直线x=-1的右侧，在直线y=-2的上侧，再结合与原点同侧得到2x+y＜2，则表示阴影部分的二元一次不等式组可求．
解答 解：由图可知，阴影部分在直线x=-1的右侧（x+1＞0），在直线y=-2的上侧（y＞-2），且与原点（0，0）在直线$\frac{x}{1}+\frac{y}{2}=1$，即2x+y=2的同侧．
∵原点坐标满足2x+y＜2，∴阴影部分点的坐标满足2x+y＜2，
则表示阴影部分的二元一次不等式组是$\left\{\begin{array}{l}{x+1＞0}\\{2x+y＜2}\\{y≥-2}\end{array}\right.$，
故选：A．
点评 本题考查简单的线性规划，考查了二元一次不等式组所表示的平面区域，是基础题．
练习册系列答案
相关题目
4．设sinx+siny=$\frac{\sqrt{2}}{2}$，则cosx+cosy的取值范围是（ ）
| A． | [0，$\frac{\sqrt{14}}{2}$] | B． | [-$\frac{\sqrt{14}}{2}$，0] | C． | [-$\frac{\sqrt{14}}{2}$，$\frac{\sqrt{14}}{2}$] | D． | [-$\frac{1}{2}$，$\frac{7}{2}$] |
2．sin$\frac{16π}{3}$的值为（ ）
| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | -$\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
9．某商场为一种跃进商品进行合理定价，将该商品按事先拟定的价格进行试销，得到如下数据：
（Ⅰ）按照上述数据，求四归直线方程$\widehat{y}$=bx+a，其中b=-20，a=$\widehat{y}$-b$\widehat{x}$；
（Ⅱ）预计在今后的销售中，销量与单位仍然服从（Ⅰ）中的关系，若该商品的成本是每件7.5元，为使商场获得最大利润，该商品的单价应定为多少元？（利润=销售收入-成本）
| 单位x（元） | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y（件） | 90 | 84 | 83 | 80 | 75 | 68 |
（Ⅱ）预计在今后的销售中，销量与单位仍然服从（Ⅰ）中的关系，若该商品的成本是每件7.5元，为使商场获得最大利润，该商品的单价应定为多少元？（利润=销售收入-成本）
3．为了参加奥运会，对自行车运动员甲、乙两人在相同的条件下进行了6次测试，测得他们的最大速度的数据如表所示：
（1）分别求甲、乙两运动员最大速度的平均数${\overline X_甲}$，${\overline X_乙}$及方差${s_甲}^2$，${s_乙}^2$；
（2）根据（1）所得数据阐明：谁参加这项重大比赛更合适．
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
（2）根据（1）所得数据阐明：谁参加这项重大比赛更合适．