题目内容
6.若函数f(x)的定义域内存在实数x,满足f(-x)=-f(x),则称f(x)为“局部奇函数”.例如:f(x)=x2+x-1在R上存在x=1,满足f(-1)=-f(1),故称f(x)=x2+x-1为“局部奇函数”.设f(x)=2x+m是定义在[-1,1]上的“局部奇函数”,则实数m的取值范围为$[-\frac{5}{4},-1]$.分析 利用局部奇函数的定义,建立方程关系,然后判断方程是否有解即可.
解答 解:根据局部奇函数的定义,f(x)=2x+m时,f(-x)=-f(x)可化为2x+2-x+2m=0,
因为f(x)的定义域为[-1,1],所以方程2x+2-x+2m=0在[-1,1]上有解,
令t=2x∈[$\frac{1}{2}$,2],则-2m=t+$\frac{1}{t}$,
设g(t)=t+$\frac{1}{t}$,则g'(t)=1-$\frac{1}{{t}^{2}}$=$\frac{{t}^{2}-1}{{t}^{2}}$,
当t∈(0,1)时,g'(t)<0,故g(t)在(0,1)上为减函数,
当t∈(1,+∞)时,g'(t)>0,故g(t)在(1,+∞)上为增函数,
所以t∈[$\frac{1}{2}$,2]时,g(t)∈[2,$\frac{5}{2}$].所以-2m∈[2,$\frac{5}{2}$],即m∈[-$\frac{5}{4}$,-1].
故答案为:$[-\frac{5}{4},-1]$
点评 本题主要考查新定义的应用,利用新定义,建立方程关系,然后利用函数性质进行求解是解决本题的关键,考查学生的运算能力.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
17.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}(x≤0)}\\{lo{{g}_{\frac{1}{2}}}{|x-1|}(x>0且x≠1)}\end{array}\right.$,若互不相等的实数a,b,c满足f(a)=f(b)=f(c),则a+b+c的取值范围是( )
| A. | (-∞,2] | B. | (-∞,1] | C. | (1,2) | D. | (2,+∞) |
14.如图所示,表示阴影部分的二元一次不等式组是( )
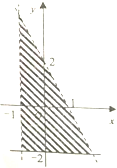

| A. | $\left\{\begin{array}{l}{x+1>0}\\{2x+y<2}\\{y≥-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+1≥0}\\{2x+y≤2}\\{y>-2}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+1≥0}\\{2x+y<2}\\{y>-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+1<0}\\{2x+y<2}\\{y>-2}\end{array}\right.$ |
11.若直线l1:x+(1+m)y=2-m与l2:mx+2y=-8平行,则实数m的值为( )
| A. | m=1或-2 | B. | m=1 | C. | m=-2 | D. | m=-$\frac{2}{3}$ |
18.满足条件|z+i|=|2+3i|的复数z在复平面上对应点的轨迹是( )
| A. | 一条直线 | B. | 两条直线 | C. | 圆 | D. | 椭圆 |