Question

（09年湖北鄂州5月模拟理）（12分）如图，已知四棱锥P―ABCD，底面ABCD为菱形，PA⊥平面ABCD，∠ABC＝60^o，E、F 分别是BC、PC的中点．

⑴证明：AE⊥PD；

⑵若H为PD上的动点，EH与平面PAD所成最大角的正
切值为，求二面角E―AF―C的余弦值．

Answer 1

解析：⑴连结AC，△ABC为正△，又E为BC中点，∴AE⊥BC又AD∥BC

∴AE⊥AD，又PA⊥平面ABCD

故AD为PD在平面ABCD内的射影，由三垂线定理知：AE⊥PD。         4分

⑵连HA，由EA⊥平面PAD知∠AHE为EH与平面PAD所成线面角            5分

而tan∠AHE＝故当AH最小即AH⊥PD时EH与平面PAD所成角最大

                                                                                                               6分

令AB＝2，则AE＝，此时

∴AH＝，由平几知识得PA＝2                                                          7分

因为PA⊥平面ABCD，PA平面PAC，所以平面PAC⊥平面ABCD

过E作EO⊥AC于O，则EO⊥平面PAC

过O作OS⊥AF于S，连结ES，则∠ESO

为二面角E―AF―C的平面角                                                                  9分

在Rt△AOE中，EO＝AE?sin30°＝，AO＝AE?cos30°＝

又F是PC的中点，在Rt△ASO中，SO＝AO?sin45°＝

又SE＝，在Rt△ESO中，cos∠ESO＝

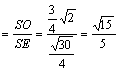
即所求二面角的余弦值为                                                                                      12分

注：向量法及其它方法可参照给分。