Question

给出下列四个命题中：
①底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥；
②与不共面的四点距离都相等的平面共有4个．
③正四棱锥侧面为锐角三角形；
④椭圆中，离心率e趋向于0，则椭圆形状趋向于扁长．
其中所有真命题的序号是

③

．

Answer 1

分析：①根据正三棱锥的定义判断．
②四个点在平面同侧不可能存在与空间不共面四点距离相等的平面，那么可分为一个点在平面一侧，另三个点在另一侧，中截面满足条件，这样的情形有4个，还有一类是二个点在平面一侧，另两个点在另一侧，这样满足条件的平面有三个，即可求出所有满足条件的平面．
③可由侧面中等腰三角形定义分析，三角形底角不会为钝角，若顶角为钝角，则构不成正四棱锥．
④在椭圆中，e越接近于1，则c越接近于a，从而b越小，因此，椭圆越扁；反之，e越接近于0，c越接近于0，从而b越接近于a，这时椭圆就接近于圆．所以椭圆离心率越大，它越扁．利用此规律即可得出结论．

解答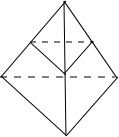：解：①显然不对，比如三条侧棱中仅有一条不与底面边长相等的情况，侧面都是等腰三角形的三棱锥但不是正三棱锥．
②一个点在平面一侧，另三个点在另一侧，这样满足条件的平面有四个，都是中截面，如图，二个点在平面一侧，另两个点在另一侧，这样满足条件的平面有三个，如图，
故与不共面的四点距离都相等的平面共有7个；故②错；
③侧面三角形底角不会为钝角，若顶角为钝角，则构不成正四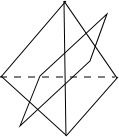棱锥，所以是锐角三角形，故③正确．
④椭圆中，离心率e趋向于0，这时椭圆就接近于圆，故④错．
故答案为：③．

点评：本题主要考查命题的真假判断与应用，棱锥的结构特征及棱锥的分类、椭圆的几何性质等，考查很全面，要求掌握要熟练，属中档题．