题目内容
 (2007•温州一模)已知函数f(x)=(1-x)ex,设Q1(x1,0),过P1(x1,f(x1))作函数y=f(x)的图象的切线与x轴交于点Q2(x2,0),再过P2(x2,f(x2))作函数y=f(x)的图象的切线与x轴交于点Q3(x3,0),…,依此下去,过Pn(xn,f(xn))(n∈N*)作函数y=f(x)的图象的切线与x轴交于点Qn+1(xn+1,0),….若x1=2,
(2007•温州一模)已知函数f(x)=(1-x)ex,设Q1(x1,0),过P1(x1,f(x1))作函数y=f(x)的图象的切线与x轴交于点Q2(x2,0),再过P2(x2,f(x2))作函数y=f(x)的图象的切线与x轴交于点Q3(x3,0),…,依此下去,过Pn(xn,f(xn))(n∈N*)作函数y=f(x)的图象的切线与x轴交于点Qn+1(xn+1,0),….若x1=2,(Ⅰ)试求出x2的值并写出xn+1与xn的关系;
( II)求证:n-1<
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| xn |
| 1 |
| 2 |
分析:(1)可通过求函数f(x)=(1-x)ex的导数来求得过Pn(xn,f(xn))(n∈N*)作函数y=f(x)的图象的切线方程的斜率,从而求得切线方程,然后可令y=0,即可得到xn+1与xn的关系;
(2)由(1)得到xn+1=xn+
-1,x1=2>1,先用数学归纳法法证明xn>1,从而得
<1,利用累加法可证得
+…+
<n-1,结合
=
,从而有
+
+…+
≤n-
;再利用
=xn+1-xn+1,可证明
+
+…+
=xn+1-x1+n=xn+1-2+n>n-1,问题即可得证明.
(2)由(1)得到xn+1=xn+
| 1 |
| xn |
| 1 |
| xn |
| 1 |
| x2 |
| 1 |
| xn |
| 1 |
| x1 |
| 1 |
| 2 |
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| xn |
| 1 |
| 2 |
| 1 |
| xn |
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| xn |
解答:解:(I)由题意得:导数为f′(x)=-xex,可求得x2=
---(3分)
过Pn(xn,f(xn))(n∈N*)作函数y=f(x)的图象的切线方程为:y-(1-xn)exn=-xnexn(x-xn),
令y=0得:-(1-xn)exn=-xnexn(xn+1-xn),即xn+1=xn+
-1---(6分)
(II)先用数学归纳法证明:xn>1
当n=1时x1=2>1成立;
假设当n=k时成立,即xk>1.
则xk+1=xk+
-1>2-1=1(基本不等式xk+
>2),则当n=k+1时也成立.
故xn>1,---(9分)
则可得
<1,故
+…+
<n-1,又
=
,则
+
+…+
≤n-
---(11分)
由(I)得
=xn+1-xn+1,则
+
+…+
=x2-x1+1+x3-x2+1+…+xn+1-xn+1=xn+1-x1+n=xn+1-2+n则 xn+1>1,则xn+1-2+n>n-1
因此,
+
+…+
>n-1.---(14分)
| 3 |
| 2 |
过Pn(xn,f(xn))(n∈N*)作函数y=f(x)的图象的切线方程为:y-(1-xn)exn=-xnexn(x-xn),
令y=0得:-(1-xn)exn=-xnexn(xn+1-xn),即xn+1=xn+
| 1 |
| xn |
(II)先用数学归纳法证明:xn>1
当n=1时x1=2>1成立;
假设当n=k时成立,即xk>1.
则xk+1=xk+
| 1 |
| xk |
| 1 |
| xk |
故xn>1,---(9分)
则可得
| 1 |
| xn |
| 1 |
| x2 |
| 1 |
| xn |
| 1 |
| x1 |
| 1 |
| 2 |
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| xn |
| 1 |
| 2 |
---(11分)
由(I)得
| 1 |
| xn |
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| xn |
因此,
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| xn |
点评:本题考查用数学归纳法证明不等式,难点有二,一在于证明xn>1的思考与证明,而在于对
=xn+1-xn+1的灵活应用,考查学生的综合分析与转化能力,属于难题.
| 1 |
| xn |

练习册系列答案
相关题目
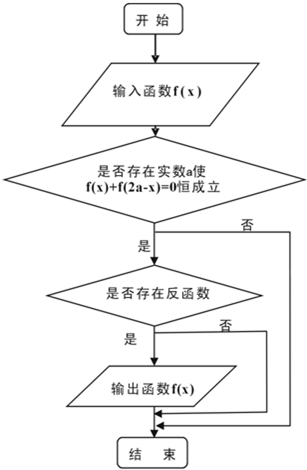 (2007•温州一模)某流程如图所示,现输入如下四个函数,则可以输出的函数是( )
(2007•温州一模)某流程如图所示,现输入如下四个函数,则可以输出的函数是( )