题目内容
设函数 ,当
,当 时,
时, 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是
A. | B. | C. | D. |
D
解析试题分析:∵ ,∴
,∴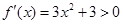 ,∴函数f(x)在R上单调递增的奇函数,又
,∴函数f(x)在R上单调递增的奇函数,又 ,∴
,∴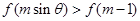 ,故当
,故当 时,
时,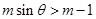 恒成立,∴当
恒成立,∴当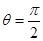 时,该式恒成立;当
时,该式恒成立;当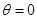 时,易知m<1;当
时,易知m<1;当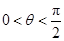 时,
时,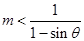 恒成立,∴
恒成立,∴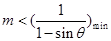 ,又
,又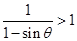 ,∴m≤1.综上所述满足题意的m的取值范围为
,∴m≤1.综上所述满足题意的m的取值范围为
考点:本题考查了导数的运用及恒成立问题
点评:对于函数的恒成立问题通常利用分离变量法,然后利用最值问题求解。

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
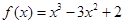 在区间
在区间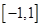 上的最大值是( )
上的最大值是( )
| A.-2 | B.0 | C.2 | D.4 |
定积分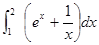 的值为 ( )
的值为 ( )
A. | B. |
C.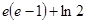 | D.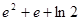 |
已知二次函数 的图象如图所示,则它与
的图象如图所示,则它与 轴所围图形的面积为:
轴所围图形的面积为:
A. | B. | C. | D. |
设 ,曲线
,曲线 在
在 处的切线与
处的切线与 轴的交点的纵坐标为
轴的交点的纵坐标为 ,则
,则 ( )
( )
| A.80 | B.32 | C.192 | D.256 |
若函数 的导函数
的导函数 ,则使得函数
,则使得函数 单调递减的一个充分不必要条件是
单调递减的一个充分不必要条件是 ( )
( )
| A.(0,1) | B.[0,2] | C.(2,3) | D.(2,4) |
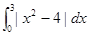 = ( )
= ( )
A. | B.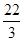 | C.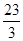 | D. |
已知 ,
, ,
, 则( )
则( )
A. | B. | C. | D. |
 是
是 的导函数,
的导函数,