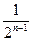题目内容
.(本小题满分14分)
已知数列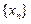 满足
满足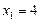 ,
,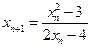 .
.
(Ⅰ)求证: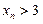 ;
;
(Ⅱ)求证: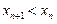 ;
;
(Ⅲ)求数列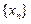 的通项公式.
的通项公式.
已知数列
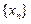 满足
满足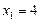 ,
,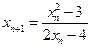 .
.(Ⅰ)求证:
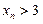 ;
;(Ⅱ)求证:
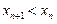 ;
;(Ⅲ)求数列
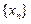 的通项公式.
的通项公式.(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)
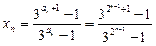
(Ⅰ)证明:用数学归纳法证明
(1)当
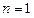 时,
时,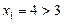 .所以结论成立.
.所以结论成立.(2)假设
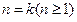 时结论成立,即
时结论成立,即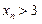 ,则
,则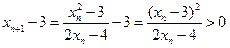 .
.所以
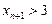 .
.即
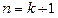 时,结论成立.
时,结论成立.由(1)(2)可知对任意的正整数
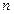 ,都有
,都有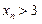 .…………………………………4分
.…………………………………4分(Ⅱ)证明:
 .
.因为
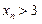 ,所以
,所以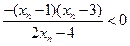 ,即
,即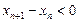 .
.所以
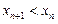 .……………………………………………………………………9分
.……………………………………………………………………9分(Ⅲ) 解:
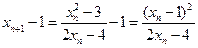 ,
,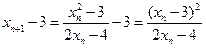 ,
,所以
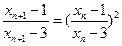 .
.又
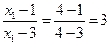 ,
,所以
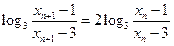 .……………………………11分
.……………………………11分又
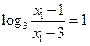 ,
,令
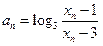 ,则数列
,则数列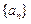 是首项为
是首项为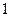 ,公比为
,公比为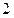 的等比数列.
的等比数列.所以
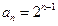 .
.由
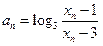 ,得
,得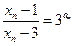 .
.所以
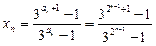 .…………………………14分
.…………………………14分
练习册系列答案
相关题目
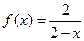 ,记数列
,记数列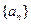 的前
的前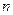 项和为
项和为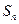 ,
,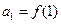 ,当
,当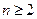 时,
时,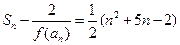
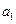 、
、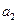 、
、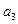 、
、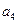 ;
;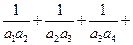 …
…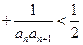
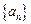 中,
中,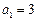 ,
,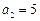 ,其前
,其前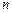 项和
项和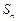 满足
满足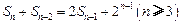 .令
.令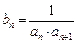 .
.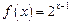 ,求证:
,求证: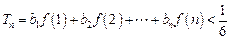 (
(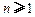 ).
).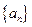 满足
满足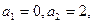
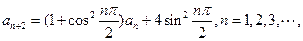
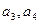 ,并求数列
,并求数列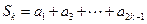 ,
,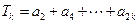 ,
,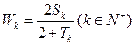 ,
,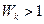 的所有k的值,并说明理由。
的所有k的值,并说明理由。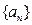 满足
满足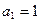 ,
,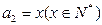 ,
,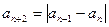
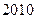 项中恰有
项中恰有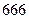 项为
项为 ,求
,求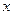
 的前
的前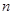 项和为
项和为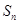 ,
,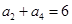 则
则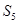 等于
等于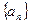 及等差数列
及等差数列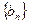 ,其中
,其中 ,公差
,公差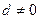 ,将这两个数列对应项相加得到一个新的数列1,1,2,…,求这个新数列的前10项之和
,将这两个数列对应项相加得到一个新的数列1,1,2,…,求这个新数列的前10项之和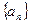
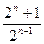 B
B C.
C.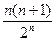 D.1-
D.1-