题目内容
(2013•北京)在△ABC中,a=3,b=2
,∠B=2∠A.
(Ⅰ)求cosA的值;
(Ⅱ)求c的值.
| 6 |
(Ⅰ)求cosA的值;
(Ⅱ)求c的值.
分析:(Ⅰ)由条件利用正弦定理和二倍角公式求得cosA的值.
(Ⅱ)由条件利用余弦定理,解方程求得c的值.
(Ⅱ)由条件利用余弦定理,解方程求得c的值.
解答:解:(Ⅰ)由条件在△ABC中,a=3,b=2
,∠B=2∠A,利用正弦定理可得
=
,即
=
=
.
解得cosA=
.
(Ⅱ)由余弦定理可得 a2=b2+c2-2bc•cosA,即 9=(2
)2+c2-2×2
×c×
,即 c2-8c+15=0.
解方程求得 c=5,或 c=3.
当c=3时,此时B=90°,A=C=45°,△ABC是等腰直角三角形,但此时不满足a2+c2=b2,故舍去.
综上,c=5.
| 6 |
| a |
| sinA |
| b |
| sinB |
| 3 |
| sinA |
2
| ||
| sin2A |
2
| ||
| 2sinAcosA |
解得cosA=
| ||
| 3 |
(Ⅱ)由余弦定理可得 a2=b2+c2-2bc•cosA,即 9=(2
| 6 |
| 6 |
| ||
| 3 |
解方程求得 c=5,或 c=3.
当c=3时,此时B=90°,A=C=45°,△ABC是等腰直角三角形,但此时不满足a2+c2=b2,故舍去.
综上,c=5.
点评:本题主要考查正弦定理和余弦定理,以及二倍角公式的应用,注意把c=3舍去,这是解题的易错点,属于中档题.

练习册系列答案
相关题目
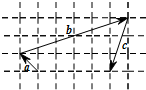 (2013•北京)向量
(2013•北京)向量