题目内容
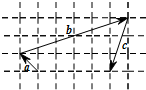 (2013•北京)向量
(2013•北京)向量| a |
| b |
| c |
| c |
| a |
| b |
| λ |
| μ |
4
4
.分析:以向量
、
的公共点为坐标原点,建立如图直角坐标系,得到向量
、
、
的坐标,结合题中向量等式建立关于λ、μ的方程组,解之得λ=-2且μ=-
,即可得到
的值.
| a |
| b |
| a |
| b |
| c |
| 1 |
| 2 |
| μ |
| λ |
解答: 解:以向量
解:以向量
、
的公共点为坐标原点,建立如图直角坐标系
可得
=(-1,1),
=(6,2),
=(-1,-3)
∵
=λ
+μ
(λ , μ∈R)
∴
,解之得λ=-2且μ=-
因此,
=
=4
故答案为:4
 解:以向量
解:以向量| a |
| b |
可得
| a |
| b |
| c |
∵
| c |
| a |
| b |
∴
|
| 1 |
| 2 |
因此,
| λ |
| μ |
| -2 | ||
-
|
故答案为:4
点评:本题给出向量
用向量
、
线性表示,求系数λ、μ的比值,着重考查了平面向量的坐标运算法则和平面向量基本定理及其意义等知识,属于基础题.
| c |
| a |
| b |

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目