题目内容
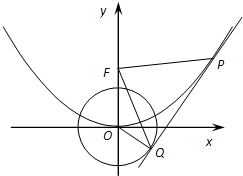 如图,O为坐标原点,点F为抛物线C1:x2=2py(p>0)的焦点,且抛物线C1上点P处的切线与圆C2:x2+y2=1相切于点Q.
如图,O为坐标原点,点F为抛物线C1:x2=2py(p>0)的焦点,且抛物线C1上点P处的切线与圆C2:x2+y2=1相切于点Q.(Ⅰ)当直线PQ的方程为x-y-
| 2 |
(Ⅱ)当正数p变化时,记S1,S2分别为△FPQ,△FOQ的面积,求
| S1 |
| S2 |
分析:(Ⅰ)设点P(x0,
),代入直线PQ的方程得一方程,再根据抛物线在P处切线斜率为1列一方程,解方程组即可求得p值;
(Ⅱ)易表示出点p处切线方程,据线圆相切得一方程,再与圆联立方程组可表示出Q坐标,据弦长公式可表示出|PQ|,利用点到直线的距离公式可表示出点F到切线PQ的距离d,则S1可表示,又S2=
|OF||xQ|=
,所以
可表示为关于x0的函数,据函数结构特点利用基本不等式即可求得其最小值.
| x02 |
| 2p |
(Ⅱ)易表示出点p处切线方程,据线圆相切得一方程,再与圆联立方程组可表示出Q坐标,据弦长公式可表示出|PQ|,利用点到直线的距离公式可表示出点F到切线PQ的距离d,则S1可表示,又S2=
| 1 |
| 2 |
| p |
| 2|x0| |
| S1 |
| S2 |
解答:解:(Ⅰ)设点P(x0,
),由x2=2py(p>0)得,y=
,求导y′=
,
因为直线PQ的斜率为1,所以
=1且x0-
-
=0,解得p=2
,
所以抛物线C1 的方程为x2=4
y.
(Ⅱ)因为点P处的切线方程为:y-
=
(x-x0),即2x0x-2py-x02=0,
根据切线与圆切,得d=r,即
=1,化简得x04=4x02+4p2,
由方程组
,解得Q(
,
),
所以|PQ|=
|xP-xQ|=
|x0-
|=
|
|,
点F(0,
)到切线PQ的距离是d=
=
,
所以S1=
|PQ|•d=
×
|
|×
=
|
|,
S2=
|OF||xQ|=
,
而由x04=4x02+4p2知,4p2=x04-4x02>0,得|x0|>2,
所以
=
|
|×
=
=
=
=
+
+3≥2
+3,当且仅当
=
时取“=”号,即x02=4+2
,此时,p=
.
所以
的最小值为2
+3.
| x02 |
| 2p |
| x2 |
| 2p |
| x |
| p |
因为直线PQ的斜率为1,所以
| x0 |
| p |
| x02 |
| 2p |
| 2 |
| 2 |
所以抛物线C1 的方程为x2=4
| 2 |
(Ⅱ)因为点P处的切线方程为:y-
| x02 |
| 2p |
| x0 |
| p |
根据切线与圆切,得d=r,即
| |-x02| | ||
|
由方程组
|
| 2 |
| x0 |
| 4-x02 |
| 2p |
所以|PQ|=
| 1+k2 |
1+
|
| 2 |
| x0 |
| ||
| p |
| x02-2 |
| x0 |
点F(0,
| p |
| 2 |
| |-p2-x02| | ||
|
| 1 |
| 2 |
| x02+p2 |
所以S1=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| p |
| x02-2 |
| x0 |
| 1 |
| 2 |
| x02+p2 |
| x02+p2 |
| 4p |
| x02-2 |
| x0 |
S2=
| 1 |
| 2 |
| p |
| 2|x0| |
而由x04=4x02+4p2知,4p2=x04-4x02>0,得|x0|>2,
所以
| S1 |
| S2 |
| x02+p2 |
| 4p |
| x02-2 |
| x0 |
| 2|x0| |
| p |
| (x02+p2)(x02-2) |
| 2p2 |
| (4x02+x04-4x02)(x02-2) |
| 2(x04-4x02) |
=
| x02(x02-2) |
| 2(x02-4) |
| x02-4 |
| 2 |
| 4 |
| x02-4 |
| 2 |
| x02-4 |
| 2 |
| 4 |
| x02-4 |
| 2 |
2+2
|
所以
| S1 |
| S2 |
| 2 |
点评:本题主要考查抛物线几何性质、直线与抛物线的位置关系,同时考查解析几何的基本思想方法和运算求解能力,综合性强,难度大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
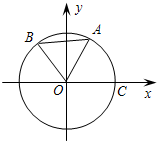 如图,O为坐标原点,点A,B,C均在⊙O上,点A
如图,O为坐标原点,点A,B,C均在⊙O上,点A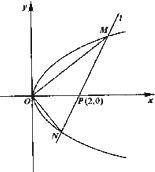 如图,O为坐标原点,过点P(2,0)且斜率为k的直线l交抛物线y2=2x于M(x1,y1),N(x2,y2)两点.
如图,O为坐标原点,过点P(2,0)且斜率为k的直线l交抛物线y2=2x于M(x1,y1),N(x2,y2)两点.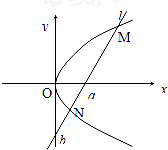 如图,O为坐标原点,直线l在x轴和y轴上的截距分别是a和b,且交抛物线y2=2px(p>0)于M(x1,y1)、N(x2,y2)两点(异于原点).
如图,O为坐标原点,直线l在x轴和y轴上的截距分别是a和b,且交抛物线y2=2px(p>0)于M(x1,y1)、N(x2,y2)两点(异于原点).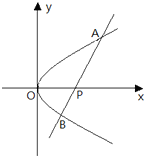 (文)如图,O为坐标原点,过点P(2,0)且斜率为k的直线l交抛物线y2=2x于A(x1,y1),B(x2,y2)两点.
(文)如图,O为坐标原点,过点P(2,0)且斜率为k的直线l交抛物线y2=2x于A(x1,y1),B(x2,y2)两点.