题目内容
已知函数f(x)=(mx+n)e-x(m,n∈R,e是自然对数的底)(1)若函数f(x)在点(1,f(1))处的切线方程为x+ey-3=0,试确定函数f(x)的单调区间;
(2)①当n=-1,m∈R时,若对于任意
 ,都有f(x)≥x恒成立,求实数m的最小值;
,都有f(x)≥x恒成立,求实数m的最小值;②当m=n=1时,设函数g(x)=xf(x)+tf'(x)+e-x(t∈R),是否存在实数a,b,c∈[0,1],使得g(a)+g(b)<g(c)?若存在,求出t的取值范围;若不存在,说明理由.
【答案】分析:(1)求导函数,利用函数f(x)在点(1,f(1))处的切线方程为x+ey-3=0,可得f(1)= ,f′(1)=-
,f′(1)=- ,从而可得函数的解析式,利用导数的正负可得函数的单调区间;
,从而可得函数的解析式,利用导数的正负可得函数的单调区间;
(2)①对于任意 ,都有f(x)≥x恒成立,等价于m≥
,都有f(x)≥x恒成立,等价于m≥ ,对于任意
,对于任意 恒成立,构造函数可得φ(x)的最大值是φ(
恒成立,构造函数可得φ(x)的最大值是φ( )和φ(2)中的较大的一个,由此可求m的最小值;
)和φ(2)中的较大的一个,由此可求m的最小值;
②假设存在a,b,c∈[0,1],使得g(a)+g(b)<g(c),则问题等价于2g(x)min<g(x)max,1求导函数,分类讨论求出函数的最值,即可求得结论.
解答:解:(1)由题意,f′(x)=
∵函数f(x)在点(1,f(1))处的切线方程为x+ey-3=0
∴f(1)= ,f′(1)=-
,f′(1)=-
∴ ,
,
∴m=1,n=1
∴f(x)=(x+1)e-x,f′(x)=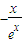
令f′(x)>0,可得x<0,令f′(x)<0,可得x>0,
∴f(x)在(0,+∞)上单调递减,在(-∞,0)上单调递增;
(2)①当n=-1,m∈R时, ,即m≥
,即m≥
对于任意 ,都有f(x)≥x恒成立,等价于m≥
,都有f(x)≥x恒成立,等价于m≥ ,对于任意
,对于任意 恒成立
恒成立
记φ(x)= ,则φ′(x)=
,则φ′(x)=
记h(x)= ,则h′(x)=
,则h′(x)= >0对于任意
>0对于任意 恒成立,
恒成立,
∴h(x)= 在
在 上单调递增
上单调递增
∵
∴φ′(x)= 在
在 上有唯一的零点x,
上有唯一的零点x,
∴x∈( ,x),φ′(x)<0,x∈(x,2),φ′(x)>0
,x),φ′(x)<0,x∈(x,2),φ′(x)>0
∴φ(x)在( ,x)上单调递减,在(x,2)上单调递增
,x)上单调递减,在(x,2)上单调递增
∴φ(x)的最大值是φ( )和φ(2)中的较大的一个
)和φ(2)中的较大的一个
∴m≥φ( )且m≥φ(2)
)且m≥φ(2)
∴m≥ +2且m≥
+2且m≥
∴m的最小值为 ;
;
②假设存在a,b,c∈[0,1],使得g(a)+g(b)<g(c),则问题等价于2g(x)min<g(x)max,
∵g(x)=xf(x)+tf'(x)+e-x=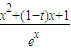 ,∴g′(x)=
,∴g′(x)=
当t≥1时,在[0,1]上g′(x)≤0,∴g(x)在[0,1]上单调递减,∴2g(1)<g(0),∴2×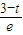 <1,∴
<1,∴ ;
;
当t≤0时,在[0,1]上g′(x)≥0,∴g(x)在[0,1]上单调递增,∴2g(0)<g(1),∴2< ,∴t<3-2e<0;
,∴t<3-2e<0;
当0<t<1时,在[0,t)上,g′(x)<0,∴g(x)在[0,t)上单调递减,在(t,1]上,g′(x)>0,∴g(x)在(t,1]上单调递增,∴2g(t)<max{g(0),g(1)}
∴2×
由(1)知f(t)= 在[0,1]上单调递减,故
在[0,1]上单调递减,故
 ,
,
∵
∴2× 无解
无解
综上所述,存在t∈(-∞,3-2e)∪(3- ,+∞),使得命题成立.
,+∞),使得命题成立.
点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,考查分类讨论的数学思想,正确求导,合理分类是关键.
 ,f′(1)=-
,f′(1)=- ,从而可得函数的解析式,利用导数的正负可得函数的单调区间;
,从而可得函数的解析式,利用导数的正负可得函数的单调区间;(2)①对于任意
 ,都有f(x)≥x恒成立,等价于m≥
,都有f(x)≥x恒成立,等价于m≥ ,对于任意
,对于任意 恒成立,构造函数可得φ(x)的最大值是φ(
恒成立,构造函数可得φ(x)的最大值是φ( )和φ(2)中的较大的一个,由此可求m的最小值;
)和φ(2)中的较大的一个,由此可求m的最小值;②假设存在a,b,c∈[0,1],使得g(a)+g(b)<g(c),则问题等价于2g(x)min<g(x)max,1求导函数,分类讨论求出函数的最值,即可求得结论.
解答:解:(1)由题意,f′(x)=

∵函数f(x)在点(1,f(1))处的切线方程为x+ey-3=0
∴f(1)=
 ,f′(1)=-
,f′(1)=-
∴
 ,
,
∴m=1,n=1
∴f(x)=(x+1)e-x,f′(x)=
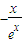
令f′(x)>0,可得x<0,令f′(x)<0,可得x>0,
∴f(x)在(0,+∞)上单调递减,在(-∞,0)上单调递增;
(2)①当n=-1,m∈R时,
 ,即m≥
,即m≥
对于任意
 ,都有f(x)≥x恒成立,等价于m≥
,都有f(x)≥x恒成立,等价于m≥ ,对于任意
,对于任意 恒成立
恒成立记φ(x)=
 ,则φ′(x)=
,则φ′(x)=
记h(x)=
 ,则h′(x)=
,则h′(x)= >0对于任意
>0对于任意 恒成立,
恒成立,∴h(x)=
 在
在 上单调递增
上单调递增∵

∴φ′(x)=
 在
在 上有唯一的零点x,
上有唯一的零点x,∴x∈(
 ,x),φ′(x)<0,x∈(x,2),φ′(x)>0
,x),φ′(x)<0,x∈(x,2),φ′(x)>0∴φ(x)在(
 ,x)上单调递减,在(x,2)上单调递增
,x)上单调递减,在(x,2)上单调递增∴φ(x)的最大值是φ(
 )和φ(2)中的较大的一个
)和φ(2)中的较大的一个∴m≥φ(
 )且m≥φ(2)
)且m≥φ(2)∴m≥
 +2且m≥
+2且m≥
∴m的最小值为
 ;
;②假设存在a,b,c∈[0,1],使得g(a)+g(b)<g(c),则问题等价于2g(x)min<g(x)max,
∵g(x)=xf(x)+tf'(x)+e-x=
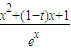 ,∴g′(x)=
,∴g′(x)=
当t≥1时,在[0,1]上g′(x)≤0,∴g(x)在[0,1]上单调递减,∴2g(1)<g(0),∴2×
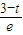 <1,∴
<1,∴ ;
;当t≤0时,在[0,1]上g′(x)≥0,∴g(x)在[0,1]上单调递增,∴2g(0)<g(1),∴2<
 ,∴t<3-2e<0;
,∴t<3-2e<0;当0<t<1时,在[0,t)上,g′(x)<0,∴g(x)在[0,t)上单调递减,在(t,1]上,g′(x)>0,∴g(x)在(t,1]上单调递增,∴2g(t)<max{g(0),g(1)}
∴2×

由(1)知f(t)=
 在[0,1]上单调递减,故
在[0,1]上单调递减,故
 ,
,∵

∴2×
 无解
无解综上所述,存在t∈(-∞,3-2e)∪(3-
 ,+∞),使得命题成立.
,+∞),使得命题成立.点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,考查分类讨论的数学思想,正确求导,合理分类是关键.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|