题目内容
已知l1、l2是过点P(-(Ⅰ)求l1的斜率k1的取值范围;
(Ⅱ)(理)若|A1B1|=![]() |A2B2|,求l1、l2的方程.
|A2B2|,求l1、l2的方程.
(文)若A1恰是双曲线的一个顶点,求|A2B2|的值.
解析:
| (Ⅰ)依题设l1、l2的斜率都存在,因为l1过点P(-
整理得(k12-1)x2+2 若k12-1=0,则方程组①只有一个解,即l1与双曲线只有一个交点与题设 矛盾,故k12-1≠0即k12≠1 所以方程②的判别式Δ=(2 又设l2的斜率为k2,l2过点P(- 两个交点,故方程组
整理得(k22-1)x2+2 同理有k22-1≠0,Δ=4(3k22-1) 因为l1⊥l2,所以k1·k2=-1 所以l1、l2与双曲线各有两个交点等价于
∴k1∈(- (Ⅱ)(理)设A1(x1,y1)、B1(x2,y2)由方程②知
所以|A1B1|2=(x1-x2)2+(y1-y2)2=(1+k12)(x1-x2)2 = 同理,由方程④可得 |A2B2|2= 由|A1B1|= 将⑤、⑥代入上式得
解得k1=± 取k1= l1:y= 取k1=- l1:y=- (Ⅱ)(文)双曲线y2-x2=1的顶点为(0,1)、(0,-1). 取A1(0,1)时,有:k1(0+ 将k2=- 记直线l2与双曲线的两交点为A2(x1,y1)、B2(x2,y2) 则|A2B2|2=(x1-x2)2+(y1-y2)2=3(x1-x2)2=3[(x1+x2)2-4x1x2] 由⑦,知x1+x2=-4 即|A2B2|=2 当取A1(0,-1)时,由双曲线y2-x2=1关于x轴的对称性,知|A2B2|=2 所以l1过双曲线的一个顶点时,|A2B2|=2 |

 名校课堂系列答案
名校课堂系列答案 ①k1≠0有两个不同的解
①k1≠0有两个不同的解 ③有两个不同的解
③有两个不同的解 整理得
整理得
 .
.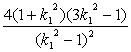 ⑤
⑤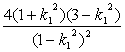 ⑥
⑥
 ,0)的两条互相垂直的直线,且l1、l2与双曲线y2-x2=1各有两个交点,分别为A1、B1和A2、B2.
,0)的两条互相垂直的直线,且l1、l2与双曲线y2-x2=1各有两个交点,分别为A1、B1和A2、B2. |A2B2|,求l1、l2的方程.
|A2B2|,求l1、l2的方程.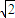 ,0)的两条互相垂直的直线,且l1、l2与双曲线y2-x2=1各有两个交点,分别为A1、B1和A2、B2.
,0)的两条互相垂直的直线,且l1、l2与双曲线y2-x2=1各有两个交点,分别为A1、B1和A2、B2. |A2B2|,求l1、l2的方程.
|A2B2|,求l1、l2的方程. ,0)的两条互相垂直的直线,且l1、l2与双曲线y2-x2=1各有两个交点,分别为A1、B1和A2、B2.
,0)的两条互相垂直的直线,且l1、l2与双曲线y2-x2=1各有两个交点,分别为A1、B1和A2、B2. |A2B2|,求l1、l2的方程.
|A2B2|,求l1、l2的方程. ,0)的两条互相垂直的直线,且l1、l2与双曲线y2-x2=1各有两个交点,分别为A1、B1和A2、B2.
,0)的两条互相垂直的直线,且l1、l2与双曲线y2-x2=1各有两个交点,分别为A1、B1和A2、B2. |A2B2|,求l1、l2的方程.
|A2B2|,求l1、l2的方程.