题目内容
5.函数f(x)=$\frac{x-1}{x+1}$的定义域是( )| A. | (-∞,-1)∪(1,+∞) | B. | (-∞,1)∪(1,∞) | C. | (-∞,-1)∪(-1,+∞) | D. | (1,+∞) |
分析 利用分母不为0,写出不等式求解即可.
解答 解:要使函数f(x)=$\frac{x-1}{x+1}$有意义,可得:x+1≠0,即x≠-1.
所以函数的定义域为:(∞,-1)∪(-1,+∞).
故选:C.
点评 本题考查函数的定义域的求法,是基础题.

练习册系列答案
相关题目
18.已知f(x)=$\left\{\begin{array}{l}{-{x}^{2},x≥0}\\{{x}^{2}+2x,x<0}\end{array}\right.$,则f(f(x))≤3的解集为( )
| A. | (-∞,-3] | B. | [-3,+∞) | C. | (-∞,$\sqrt{3}$] | D. | [$\sqrt{3}$,+∞) |
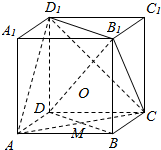 如图所示,在正方体ABCD-A1B1C1D1中,B1D与平面ACD1交于点O,BD与平面ACD1交于点M,求证:M,O,D1三点共线.
如图所示,在正方体ABCD-A1B1C1D1中,B1D与平面ACD1交于点O,BD与平面ACD1交于点M,求证:M,O,D1三点共线.