题目内容
设a=(1+cosα,sinα),b=(1-cosβ,sinβ),c=(1,0),α∈(0,π),β∈(π,2π),a与c的夹角为θ1,b与c的夹角为θ2,且θ1-θ2=![]() ,求sin
,求sin![]() 的值.
的值.
答案:
解析:
解析:
|
解:a=(2cos2 b=(2sin2 又θ1-θ2= 所以sin |

练习册系列答案
相关题目
 ,2sin
,2sin ,2sin
,2sin .
.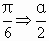 -
- =-
=- .
. .
. },B={x||x-1|<a,a>0
},B={x||x-1|<a,a>0 ,若A
,若A B=A,求a的取值范围.
B=A,求a的取值范围.