Question

设a，b∈R，A＝{(x，y)|x＝n，y＝na＋b，n∈Z}，B＝{(x，y)|x＝m，y＝3m²＋15，m∈Z}，C＝{(x，y)|x²＋y²≤144}是平面xOy内点的集合，讨论是否存在a，b，使得：

(1)A∩B≠．

(2)(a，b)∈C同时成立．

Answer 1

答案：
解析：

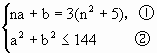解：由已知，命题等价于是否有解，在aOb坐标系中，①表示直线，②表示以原点为圆心，R为半径的圆(包括圆周)，方程组有解的充要条件是圆心到直线的距离不大于圆的半径，即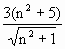≤12．即(n2－3)2≤0，所以n2＝3，这与n∈Z矛盾，所以符合条件的a，b不存在．