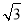题目内容
如图,在四棱锥P-ABCD中,已知PB⊥底面ABCD,BC⊥AB,AD∥BC,AB=AD=2,CD⊥PD,异面直线PA和CD所成角等于60°.

(1)求证:面PCD⊥面PBD;
(2)求直线PC和平面PAD所成角的正弦值的大小;
(3)在棱PA上是否存在一点E,使得二面角A-BE-D的余弦值为 ?若存在,指出点E在棱PA上的位置,若不存在,说明理由.
?若存在,指出点E在棱PA上的位置,若不存在,说明理由.
(1)见解析(2)存在
【解析】(1)证明:PB⊥底面ABCD,∴PD⊥CD,
又∵CD⊥PD,PD∩PB=P,PD,PB?平面PBD.
∴CD⊥平面PBD,又CD?平面PCD,
∴平面PCD⊥平面PBD.
(2)如图,以B为原点,BA,BC,BP所在直线分别为x,y,z轴,建立空间直角坐标系,
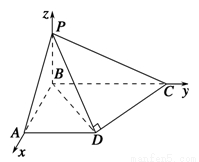
设BC=a,BP=b,则B(0,0,0),A(2,0,0),C(0,a,0),
D(2,2,0),P(0,0,b).
∵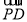 =(2,2,-b),
=(2,2,-b),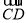 =(2,2-a,0),CD⊥PD,
=(2,2-a,0),CD⊥PD,
∴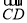 ·
·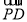 =0,∴4+4-2a=0,a=4,
=0,∴4+4-2a=0,a=4,
又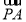 =(2,0,-b),
=(2,0,-b),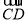 =(2,-2,0),
=(2,-2,0),
异面直线PA和CD所成角等于60°,
∴ =
=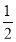 ,
,
即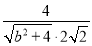 =
=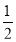 ,解得b=2,
,解得b=2,
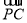 =(0,4,-2),
=(0,4,-2),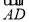 =(0,2,0),
=(0,2,0),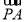 =(2,0,-2).
=(2,0,-2).
设平面PAD的一个法向量为n1=(x1,y1,z1),
则由 得
得
取n1=(1,0,1),
∵sin θ=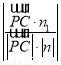 =
=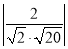 =
=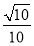 ,∴直线PC和平面PAD所成角的正弦值为
,∴直线PC和平面PAD所成角的正弦值为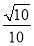 .
.
(3)解 假设存在,设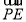 =λ
=λ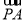 ,且E(x,y,z),则(x,y,z-2)=λ(2,0,-2),E(2λ,0,2-2λ),设平面DEB的一个法向量为n2=(x2,y2,z2),
,且E(x,y,z),则(x,y,z-2)=λ(2,0,-2),E(2λ,0,2-2λ),设平面DEB的一个法向量为n2=(x2,y2,z2),
则由 得
得
取n2=(λ-1,1-λ,λ),
又平面ABE的法向量n3=(0,1,0),
由cos θ=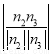 =
=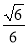 ,得
,得 =
=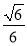 ,解得λ=
,解得λ=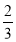 或λ=2(不合题意).
或λ=2(不合题意).
∴存在这样的E点,E为棱PA上的靠近A的三等分点.