题目内容
(12分)
设函数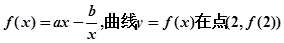 处的切线方程为
处的切线方程为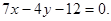
(Ⅰ)求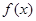 的解析式;
的解析式;
(Ⅱ)证明:曲线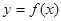 上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.
上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.
【答案】

(II)设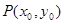 为曲线上任一点,由
为曲线上任一点,由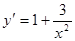 知曲线在点
知曲线在点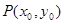 处的切线方程为
处的切线方程为
即
令 ,从而得切线与直线
,从而得切线与直线 的交点坐标为(0,
的交点坐标为(0, ).
).
令y=x得y=x=2x0,从而得切线与直线y=x的交点坐标为(2x0,2x0).…………10分
所以点 所围成的三角形面积为
所围成的三角形面积为
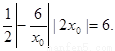
故曲线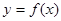 上任一点处的切线与直线
上任一点处的切线与直线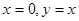 所围成的三角形的面积为定值,此定值为6. ……12分
所围成的三角形的面积为定值,此定值为6. ……12分
【解析】略

练习册系列答案
相关题目
 ,其中
,其中 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 轴
轴 为
为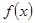 的极值点,求
的极值点,求 可作曲线
可作曲线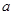 的取值范围。
的取值范围。