题目内容
(本小题满分12分)设函数 ,其中
,其中 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 轴
轴
(1)若 为
为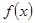 的极值点,求
的极值点,求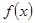 的解析式
的解析式
(2)若过点 可作曲线
可作曲线 的三条不同切线,求
的三条不同切线,求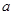 的取值范围。
的取值范围。
【答案】
 ,
,
【解析】解:由
又由曲线 处的切线方程为
处的切线方程为 轴,得
轴,得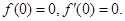
故 …………………………… 2分
…………………………… 2分
(I)又 ,所以
,所以 ,
, …………………………… 4分
…………………………… 4分
(II) 处的切线方程为
处的切线方程为
 ,而点(0,2)在切线上,所以
,而点(0,2)在切线上,所以 ,
,
化简得 ……………… 6分
……………… 6分
过点(0,2)可作 的三条切线,等价于方程
的三条切线,等价于方程
有三个相异的实根,即等价于方程 有三个相异的实根.
有三个相异的实根.
 故有
故有
|
|
|
0 |
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
↗ |
极大值 |
↘ |
极小值 |
↗ |
由 的单调性知:要使
的单调性知:要使 有三个相异的实根,当且仅当
有三个相异的实根,当且仅当 时满足,即
时满足,即 ,
, .
.
 的取值范围是
的取值范围是 ……………………………………………… 12分
……………………………………………… 12分

练习册系列答案
相关题目





