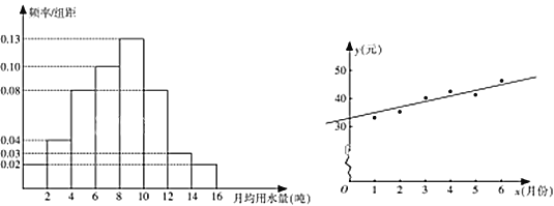
题目内容
【题目】设函数f(x)=a2x2(a>0),g(x)=bln x.
(1)若函数y=f(x)图象上的点到直线x-y-3=0距离的最小值为2![]() ,求a的值;
,求a的值;
(2)对于函数f(x)与g(x)定义域上的任意实数x,若存在常数k,m,使得f(x)≥kx+m和g(x)≤kx+m都成立,则称直线y=kx+m为函数f(x)与g(x)的“分界线”.设a=![]() ,b=e,试探究f(x)与g(x)是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
,b=e,试探究f(x)与g(x)是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:
(1)由题意结合导函数的性质得到关于实数![]() 的方程,解方程可得实数a的值为
的方程,解方程可得实数a的值为![]() .
.
(2)构造函数![]() ,结合题意和函数的性质可得f(x)与g(x)的图象有公共点
,结合题意和函数的性质可得f(x)与g(x)的图象有公共点![]() .由“分界线”的定义可得x2-2kx-e+2k
.由“分界线”的定义可得x2-2kx-e+2k![]() ≥0在x∈R上恒成立.据此可得
≥0在x∈R上恒成立.据此可得![]() ,然后结合导函数的性质证明
,然后结合导函数的性质证明![]() 恒成立即可.
恒成立即可.
试题解析:
(1)因为f(x)=a2x2,所以f′(x)=2a2x,
令f′(x)=2a2x=1,
得x=![]() ,此时y=
,此时y=![]() ,
,
则点![]() 到直线x-y-3=0的距离为2
到直线x-y-3=0的距离为2![]() ,
,
即2![]() =
=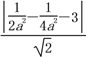 ,解得a=
,解得a=![]() (负值舍去).
(负值舍去).
(2)设F(x)=f(x)-g(x)=![]() x2-eln x(x>0),
x2-eln x(x>0),
则F′(x)=x-![]() =
=![]() =
=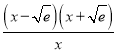 .
.
所以当0<x<![]() 时,F′(x)<0;当x>
时,F′(x)<0;当x>![]() 时,F′(x)>0.
时,F′(x)>0.
因此x=![]() 时,F(x)取得最小值0,
时,F(x)取得最小值0,
则f(x)与g(x)的图象在x=![]() 处有公共点
处有公共点![]() .
.
设f(x)与g(x)存在“分界线”,
方程为y-![]() =k(x-
=k(x-![]() ),即y=kx+
),即y=kx+![]() -k
-k![]() ,
,
由f(x)≥kx+![]() -k
-k![]() 在x∈R上恒成立,
在x∈R上恒成立,
则x2-2kx-e+2k![]() ≥0在x∈R上恒成立.
≥0在x∈R上恒成立.
所以Δ=4k2-4(2k![]() -e)=4k2-8k
-e)=4k2-8k![]() +4e=4(k-
+4e=4(k-![]() )2≤0成立,因此k=
)2≤0成立,因此k=![]() .
.
下面证明g(x)≤![]() x-
x-![]() (x>0)恒成立.
(x>0)恒成立.
设G(x)=eln x-x![]() +
+![]() ,
,
则G′(x)=![]() -
-![]() =
=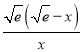 .
.
所以当0<x<![]() 时,G′(x)>0;当x>
时,G′(x)>0;当x>![]() 时,G′(x)<0.
时,G′(x)<0.
因此x=![]() 时,G(x)取得最大值0,
时,G(x)取得最大值0,
则g(x)≤![]() x-
x-![]() (x>0)成立.
(x>0)成立.
故所求“分界线”方程为y=![]() x-
x-![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案