题目内容

设函数f(x)=的图象关于直线y=x对称.

（1）求m的值；

（2）若直线y=a(a∈R)与f(x)的图象无公共点，且f(|t-2|+)＜2a+f(4a)，求实数t的取值范围.

解:（1）由y=得x=

∴f-1(x)=

由已知得，f(x)=f-1(x),∴m=1.从而f(x)=.

（2）由（1）知，f(x)=1+≠1,即f（x）值域为(-∞,1)∪(1,+∞),

∴由已知得:a=1.于是

f(|t-2|+)＜2a+f(4a)f(|t-2|+)＜2+f(4)=4,

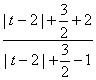∴＜4,即|t-2|+＜4|t-2|+2，即|t-2|＞，∴t＜或t＞.

练习册系列答案
相关题目
已知函数f(x)=
lnx
x
的图象为曲线C，函数g(x)=
1
2
ax+b的图象为直线l．
（Ⅰ） 设m＞0，当x∈（m，+∞）时，证明：(x+m)ln
x
m
-2(x-m)＞0
（Ⅱ） 设直线l与曲线C的交点的横坐标分别为x1，x2，且x1≠x2，求证：（x1+x2）g（x1+x2）＞2．
已知函数f(x)=
ax
b
的图象过点A(4，
1
2
)和B（5，1）．
①求函数f（x）的解析式；②函数f（x）的反函数；③设an=log2f（n），n是正整数，是数列的前项和Sn，解关于的不等式an≤Sn．

设函数f(x)＝的图象如下图所示，则a、b、c的大小关系是

[　　]
A．

a＞b＞c

B．

a＞c＞b

C．

b＞a＞c

D．

c＞a＞b

设函数f(x)＝的图象如下图所示，则a、b、c的大小关系是

[　　]

A．a＞b＞c

B．a＞c＞b

C．b＞a＞c

D．c＞a＞b

设函数f(x)=ex的反函数为g(x),点P(x1,y1),Q(x2,y2)分别为函数f(x)和g(x)图象上的两个动点.

(1)求函数h(x)=x2-g(x)的极小值;

(2)设函数f(x)的图象为C1,g(x)的图象为C2,过点P,Q的直线为l,当直线l为曲线C1和曲线C2的公切线时,求x1与x2满足的关系式及x1的取值范围.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网