题目内容
已知椭圆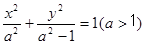 的左右焦点为
的左右焦点为 ,抛物线C:
,抛物线C: 以F2为焦点且与椭圆相交于点
以F2为焦点且与椭圆相交于点 、
、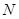
 ,点
,点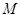 在
在 轴上方,直线
轴上方,直线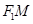 与抛物线
与抛物线 相切.
相切.
(1)求抛物线 的方程和点
的方程和点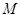 、
、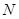 的坐标;
的坐标;
(2)设A,B是抛物线C上两动点,如果直线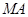 ,
, 与
与 轴分别交于点
轴分别交于点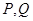 .
.  是以
是以 ,
,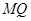 为腰的等腰三角形,探究直线AB的斜率是否为定值?若是求出这个定值,若不是说明理由.
为腰的等腰三角形,探究直线AB的斜率是否为定值?若是求出这个定值,若不是说明理由.
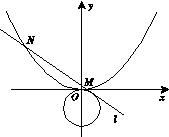
(1)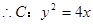 M、N的坐标分别为(1,2)、(1,-2)。
M、N的坐标分别为(1,2)、(1,-2)。
(2)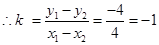 为定值
为定值
解析试题分析:解:(1)由椭圆方程得半焦距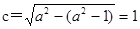 1分
1分
所以椭圆焦点为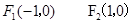
又抛物线C的焦点为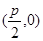
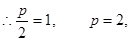
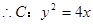 3分
3分
∵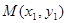 在抛物线C上,
在抛物线C上,
∴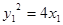 ,直线
,直线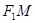 的方程为
的方程为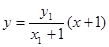 4分
4分
代入抛物线C得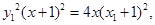
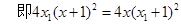
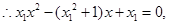 5分
5分
∵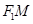 与抛物线C相切,
与抛物线C相切,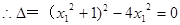 , 6分
, 6分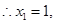 ∴ M、N的坐标分别为(1,2)、(1,-2)。 7分
∴ M、N的坐标分别为(1,2)、(1,-2)。 7分
(2)直线AB的斜率为定值—1.
证明如下:设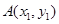 ,
,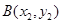 ,
,
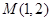 ,A、B在抛物线
,A、B在抛物线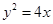 上,
上,
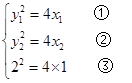
由①-③得,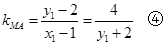
由②-③得,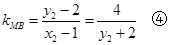 10分
10分
因为 是以MP,MQ为腰的等腰三角形,所以
是以MP,MQ为腰的等腰三角形,所以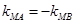 10分
10分
由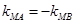 得
得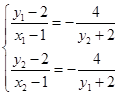 化简整理,
化简整理,
得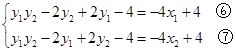
由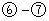 得:
得: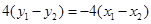
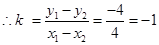 为定值 14分
为定值 14分
解法二:设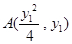 ,
,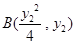 6分
6分
则
 ,
,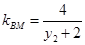 8分
8分
因为 是以MP,MQ为腰的等腰三角形,所以
是以MP,MQ为腰的等腰三角形,所以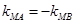 10分
10分
即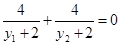
所以 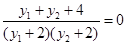
所以,由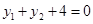 得
得 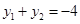 12分
12分
所以,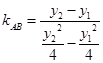
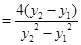

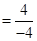
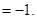
所以,直线AB的斜率为定值,这个定值为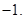 14分
14分
考点:直线与抛物线的位置关系
点评:主要是考查了抛物线方程的方程的求解以及直线与抛物线的位置关系的运用,属于中档题。

练习册系列答案
相关题目
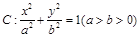 ,直线l为圆
,直线l为圆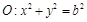 的一条切线,且经过椭圆C的右焦点,直线l的倾斜角为
的一条切线,且经过椭圆C的右焦点,直线l的倾斜角为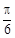 ,记椭圆C的离心率为e.
,记椭圆C的离心率为e.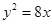 的焦点为右焦点,且经过点A(2,3).
的焦点为右焦点,且经过点A(2,3). 分别为椭圆的左右焦点,求
分别为椭圆的左右焦点,求 的角平分线所在直线的方程.
的角平分线所在直线的方程.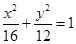 上找一点,使这一点到直线
上找一点,使这一点到直线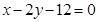 的距离为最小,并求最小值。
的距离为最小,并求最小值。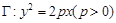 的焦点与椭圆
的焦点与椭圆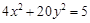 的右焦点重合.(Ⅰ)求抛物线
的右焦点重合.(Ⅰ)求抛物线 的方程;
的方程;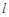 恒过点
恒过点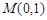 与抛物线
与抛物线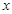 轴交于C点,请你观察并判断:在线段MA,MB,MC,AB中,哪三条线段的长总能构成等比数列?说明你的结论并给出证明.
轴交于C点,请你观察并判断:在线段MA,MB,MC,AB中,哪三条线段的长总能构成等比数列?说明你的结论并给出证明.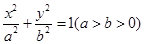 的左、右焦点分别为F1,F2,椭圆的离心率为
的左、右焦点分别为F1,F2,椭圆的离心率为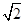 :2.(1)过点C(-1,0)且以向量
:2.(1)过点C(-1,0)且以向量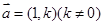 为方向向量的直线
为方向向量的直线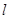 交椭圆于不同两点A、B,若
交椭圆于不同两点A、B,若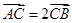 ,则当△OAB的面积最大时,求椭圆的方程。
,则当△OAB的面积最大时,求椭圆的方程。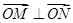 ,过原点O作直线MN的垂线OD,垂足为D,求点D的轨迹方程.
,过原点O作直线MN的垂线OD,垂足为D,求点D的轨迹方程.
 ,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值
,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值 轴上,且过点
轴上,且过点 .
.
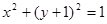 相切的直线
相切的直线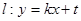 交抛物线于不同的两点
交抛物线于不同的两点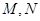 若抛物线上一点
若抛物线上一点 满足
满足
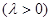 ,求
,求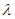 的取值范围.
的取值范围.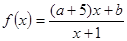 在
在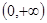 上是增函数;命题q:方程
上是增函数;命题q:方程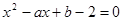 有两个不相等的负实数根。求使得p
有两个不相等的负实数根。求使得p q是真命题的实数对
q是真命题的实数对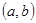 为坐标的点的轨迹图形及其面积。
为坐标的点的轨迹图形及其面积。