题目内容
（2013•深圳一模）已知两点F1（-1，0）及F2（1，0），点P在以F1、F2为焦点的椭圆C上，且|PF1|、|F1F2|、|PF2|构成等差数列．（1）求椭圆C的方程；
（2）如图，动直线l：y=kx+m与椭圆C有且仅有一个公共点，点M，N是直线l上的两点，且F1M⊥l，F2N⊥l．求四边形F1MNF2面积S的最大值．
分析：（1）依题意，设椭圆C的方程为
+
=1，c=1．再利用|PF1|、|F1F2|、|PF2|构成等差数列，即可得到a，利用b2=a2-c2得到a即可得到椭圆的方程；
（2）将直线l的方程y=kx+m代入椭圆C的方程3x2+4y2=12中，得到关于x的一元二次方程，由直线l与椭圆C仅有一个公共点知，△=0，即可得到m，k的关系式，利用点到直线的距离公式即可得到d1=|F1M|，d2=|F2N|．
法一：当k≠0时，设直线l的倾斜角为θ，则|d1-d2|=|MN|×|tanθ|，即可得到四边形F1MNF2面积S的表达式，利用基本不等式的性质即可得出S的最大值；
法二：利用d1及d2表示出
+
及d1d2，进而得到S2=
(d12+d22+2d1d2)=
，再利用二次函数的单调性即可得出其最大值．
| x2 |
| a2 |
| y2 |
| b2 |
（2）将直线l的方程y=kx+m代入椭圆C的方程3x2+4y2=12中，得到关于x的一元二次方程，由直线l与椭圆C仅有一个公共点知，△=0，即可得到m，k的关系式，利用点到直线的距离公式即可得到d1=|F1M|，d2=|F2N|．
法一：当k≠0时，设直线l的倾斜角为θ，则|d1-d2|=|MN|×|tanθ|，即可得到四边形F1MNF2面积S的表达式，利用基本不等式的性质即可得出S的最大值；
法二：利用d1及d2表示出
| d | 2 1 |
| d | 2 2 |
| 1 |
| k2+1 |
| 16k2+12 |
| (k2+1)2 |
解答：解：（1）依题意，设椭圆C的方程为
+
=1．
∵|PF1|、|F1F2|、|PF2|构成等差数列，∴2a=|PF1|+|PF|2=2|F1F2|=4，a=2．
又∵c=1，∴b2=3．∴椭圆C的方程为
+
=1．
（2）将直线l的方程y=kx+m代入椭圆C的方程3x2+4y2=12中，得（4k2+3）x2+8kmx+4m2-12=0．
由直线l与椭圆C仅有一个公共点知，△=64k2m2-4（4k2+3）（4m2-12）=0，
化简得：m2=4k2+3．
设d1=|F1M|=
，d2=|F2N|=
，
法一：当k≠0时，设直线l的倾斜角为θ，
则|d1-d2|=|MN|×|tanθ|，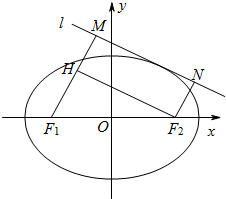
∴|MN|=|
|，S=
|
|(d1+d2)=|
|=
=
=
，
∵m2=4k2+3，∴当k≠0时，|m|＞
，|m|+
＞
+
=
，S＜2
．
当k=0时，四边形F1MNF2是矩形，S=2
．
所以四边形F1MNF2面积S的最大值为2
．
法二：∵d12+d22=(
)2+(
)2=
=
，d1d2=
•
=
=
=3．
∴|MN|=
=
=
．
四边形F1MNF2的面积S=
|MN|(d1+d2)=
(d1+d2)，
S2=
(d12+d22+2d1d2)=
=16-4(
-2)2≤12．
当且仅当k=0时，S2=12，S=2
，故Smax=2
．
所以四边形F1MNF2的面积S的最大值为2
．
| x2 |
| a2 |
| y2 |
| b2 |
∵|PF1|、|F1F2|、|PF2|构成等差数列，∴2a=|PF1|+|PF|2=2|F1F2|=4，a=2．
又∵c=1，∴b2=3．∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
（2）将直线l的方程y=kx+m代入椭圆C的方程3x2+4y2=12中，得（4k2+3）x2+8kmx+4m2-12=0．
由直线l与椭圆C仅有一个公共点知，△=64k2m2-4（4k2+3）（4m2-12）=0，
化简得：m2=4k2+3．
设d1=|F1M|=
| |-k+m| | ||
|
| |k+m| | ||
|
法一：当k≠0时，设直线l的倾斜角为θ，
则|d1-d2|=|MN|×|tanθ|，
∴|MN|=|
| d1-d2 |
| k |
| 1 |
| 2 |
| d1-d2 |
| k |
| d12-d22 |
| 2k |
| 2|m| |
| k2+1 |
| 2|m| | ||
|
| 8 | ||
|m|+
|
∵m2=4k2+3，∴当k≠0时，|m|＞
| 3 |
| 1 |
| |m| |
| 3 |
| 1 | ||
|
| 4 |
| 3 |
| 3 |
| 3 |
当k=0时，四边形F1MNF2是矩形，S=2
| 3 |
所以四边形F1MNF2面积S的最大值为2
| 3 |
法二：∵d12+d22=(
| |-k+m| | ||
|
| |k+m| | ||
|
| 2(m2+k2) |
| k2+1 |
| 2(5k2+3) |
| k2+1 |
| |-k+m| | ||
|
| |k+m| | ||
|
| |m2-k2| |
| k2+1 |
| 3k2+3 |
| k2+1 |
∴|MN|=
| F1F22-(d1-d2)2 |
| 4-(d12+d22-2d1d2) |
| 2 | ||
|
四边形F1MNF2的面积S=
| 1 |
| 2 |
| 1 | ||
|
S2=
| 1 |
| k2+1 |
| 16k2+12 |
| (k2+1)2 |
| 1 |
| k2+1 |
当且仅当k=0时，S2=12，S=2
| 3 |
| 3 |
所以四边形F1MNF2的面积S的最大值为2
| 3 |
点评：本题主要考查椭圆的方程与性质、直线方程、直线与椭圆的位置关系、等差数列、二次函数的单调性、基本不等式的性质等基础知识，考查运算能力、推理论证以及分析问题、解决问题的能力，考查数形结合、化归与转化思想．
练习册系列答案
相关题目