题目内容
电流强度 (安)随时间
(安)随时间 (秒)变化的函数
(秒)变化的函数
 的
的
图象如右图所示,则当 时,电流强度是( )
时,电流强度是( )
A. 安 安 | B. 安 安 |
C.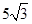 安 安 | D. 安 安 |
B
解析试题分析:通过函数的图象求出满足条件的A,周期T,利用周期公式求出ω,根据函数的图象过的特殊点求出φ值,代入给出函数的解析式,然后将 秒代入,求出题目所有的电流强度。解:由函数图象可知函数的最大值为10,最小值为-10,
秒代入,求出题目所有的电流强度。解:由函数图象可知函数的最大值为10,最小值为-10,
又由A>0,∴A=10,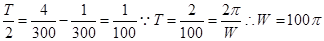 ∴I=10sin(100πt+φ),
∴I=10sin(100πt+φ), ∴I=10sin(100πt+
∴I=10sin(100πt+ ),故可知当当
),故可知当当 时,电流强度是2,故选B.
时,电流强度是2,故选B.
考点:函数解析式
点评:已知函数图象求函数y=Asin(ωx+φ)(A>0,ω>0)的解析式时,常用的解题方法是待定系数法,由图中的最大值或最小值确定A,由周期确定ω,由适合解析式的点的坐标来确定φ,但由图象求得的y=Asin(ωx+φ)(A>0,ω>0)的解析式一般不唯一,只有限定φ的取值范围,才能得出唯一解,否则φ的值不确定,解析式也就不唯一

练习册系列答案
相关题目
函数 的定义域为 ( )
的定义域为 ( )
A. | B. | C. | D.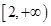 |
把函数 的图像向左平移
的图像向左平移 个单位,所得曲线的一部分
个单位,所得曲线的一部分
如图示,则 的值分别为
的值分别为
A. | B. | C. | D. |
若f(x)为R上的奇函数,给出下列四个说法:
①f(x)+f(-x)=0 ; ②f(x)-f(-x)=2f(x);
③f(x)·f(-x)<0; ④ 。其中一定正确的有( )
。其中一定正确的有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
下列函数在其定义域内,既是奇函数又存在零点的是( )
A. | B. |
C. | D.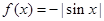 |
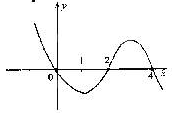
已知函数 ,其导函数
,其导函数 的图象如图所示,则
的图象如图所示,则 ( )
( )
| A.在(-∞,0)上为减函数 | B.在 0处取极小值 0处取极小值 |
| C.在(4,+∞)上为减函数 | D.在 2处取极大值 2处取极大值 |
已知函数 ,若
,若 互不相等,且
互不相等,且 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
函数 定义如下:对任意
定义如下:对任意 ,当
,当 为有理数时,
为有理数时, ;当
;当 为无理数时,
为无理数时, ;则称函数
;则称函数 为定义在实数上的狄利克雷拓展函数.下列关于函数
为定义在实数上的狄利克雷拓展函数.下列关于函数 说法错误的是( )
说法错误的是( )
A. 的值域为 的值域为 |
B. 是偶函数 是偶函数 |
C. 是周期函数且 是周期函数且 是 是 的一个周期 的一个周期 |
D. 在实数集上的任何区间都不是单调函数 在实数集上的任何区间都不是单调函数 |
 的部分图象大致是( )
的部分图象大致是( )