题目内容
{an}是公差为1的等差数列，{bn}是公比为2的等比数列，Pn，Qn分别是{an}，{bn}的前n项和，且a6=b3，P10=Q1+45．
（I）求{an}的通项公式；
（II）若Pn＞b6，求n的取值范围．
解：（I）由题意，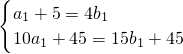
∴a1=3，b1=2
∴an=n+2；
（II）
若Pn＞b6，∴
∴n≥10．
分析：（I ）根据条件a6=b3，P10=Q1+45．可建立方程组，从而可求{an}的通项公式；
（II）先表示出Pn，b6，根据Pn＞b6，可建立不等式，从而可求n的取值范围．
点评：本题以数列为载体，考查等差数列、等比数列的通项与求和问题，考查解不等式，属于中档题．
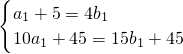
∴a1=3，b1=2
∴an=n+2；
（II）
若Pn＞b6，∴
∴n≥10．
分析：（I ）根据条件a6=b3，P10=Q1+45．可建立方程组，从而可求{an}的通项公式；
（II）先表示出Pn，b6，根据Pn＞b6，可建立不等式，从而可求n的取值范围．
点评：本题以数列为载体，考查等差数列、等比数列的通项与求和问题，考查解不等式，属于中档题．
练习册系列答案
名校联盟快乐课堂系列答案
黄冈创优卷系列答案
相关题目