题目内容
若函数f(x)对定义域中任意x均满足f(x)+f(2a-x)=2b,则称函数y=f(x)的图象关于点(a,b)对称.
(1)已知函数f(x)=
的图象关于点(0,1)对称,求实数m的值;
(2)已知函数g(x)在R上的图象关于点(0,1)对称,且当x∈(0,+∞)时,g(x)=x2-2x,求函数g(x)在R上的解析式.
(1)已知函数f(x)=
| x2+mx+m | x |
(2)已知函数g(x)在R上的图象关于点(0,1)对称,且当x∈(0,+∞)时,g(x)=x2-2x,求函数g(x)在R上的解析式.
分析:(1)利用函数f(x)=
的图象关于点(0,1)对称,可得f(x)+f(-x)=2,代入解析式,即可求得m的值;
(2)利用函数g(x)在(-∞,0)∪(0,+∞)上的图象关于点(0,1)对称,可得g(x)+g(-x)=2,根据x∈(0,+∞)时的解析式,即可求得结论;
| x2+mx+m |
| x |
(2)利用函数g(x)在(-∞,0)∪(0,+∞)上的图象关于点(0,1)对称,可得g(x)+g(-x)=2,根据x∈(0,+∞)时的解析式,即可求得结论;
解答:解:(1)∵函数f(x)=
的图象关于点(0,1)对称,
∴f(x)+f(-x)=2,
即:
+
=2,
解得m=1
(2)x<0时,-x>0,且g(x)+g(-x)=2,
∵当x∈(0,+∞)时,g(x)=x2-2x,
所以g(x)=2-g(-x)=-x2-2x+2
当x=0时,g(0)+g(-0)=2⇒g(0)=1;
因此g(x)=
| x2+mx+m |
| x |
∴f(x)+f(-x)=2,
即:
| x2+mx+m |
| x |
| x2-mx+m |
| -x |
解得m=1
(2)x<0时,-x>0,且g(x)+g(-x)=2,
∵当x∈(0,+∞)时,g(x)=x2-2x,
所以g(x)=2-g(-x)=-x2-2x+2
当x=0时,g(0)+g(-0)=2⇒g(0)=1;
因此g(x)=
|
点评:本题考查函数的对称性,考查函数的解析式,考查恒成立问题,正确求出函数的最值是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 图象的对称中心是(1,1)
图象的对称中心是(1,1) ,则函数f(x)=
,则函数f(x)=
 对任意的x1≠x2都有
对任意的x1≠x2都有 ,则实数a的
,则实数a的 ]
]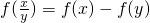 ,则不等式
,则不等式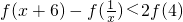 的解为
的解为