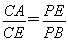Question

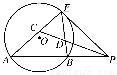
如图，AB是⊙O的直径，BC是⊙O的切线，B为切点，OC平行于弦AD，连结CD.

(1)求证：CD是⊙O的切线；

(2)过点D作DE⊥AB于点E，交AC于点P，求证：P点平分线段DE.

 

Answer 1

（1）见解析（2）见解析

【解析】(1)连结OD，

∵OC∥AD，

∴∠1＝∠ADO，∠2＝∠DAO.

∵OA＝OD，

∴∠ADO＝∠DAO，

∴∠1＝∠2.

∵OC＝OC，OB＝OD，

∴△DOC≌△BOC，

∴∠ODC＝∠OBC.

∵OB是⊙O的半径，BC是⊙O的切线，

∴BC⊥OB，∴∠OBC＝90°，

∴∠ODC＝90°，∴CD⊥OD.

又∵OD是⊙O的半径，∴CD是⊙O的切线．

(2)证法一：过点A作⊙O的切线AF，交CD的延长线于点F，则FA⊥AB.

∵DE⊥AB，由(1)知CB⊥AB，

∴FA∥DE∥CB，∴.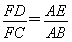

在△FAC中，∵DP∥FA，∴.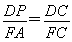

∵FA，FD是⊙O的切线，∴FA＝FD，

∴，∴

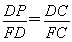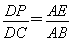
在△ABC中，∵EP∥BC，∴.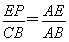

∵CD，CB是⊙O的切线，∴CB＝CD，

∴.

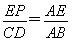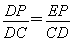∴，∴DP＝EP.

∴点P平分线段DE.

证法二：辅助线同上．

由(1)及已知条件知BC，CD，AF为⊙O的切线，B，D，A为切点，

∴CB＝CD，FA＝FD.

设CD＝m，FD＝n.

∵DE⊥AB，∴AF∥DE∥BC.

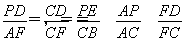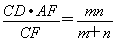∴，即PD＝，PE＝，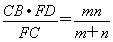

∴PD＝PE，因此P点平分线段DE.