Question

 [2012·江西卷] 如图1－7，在梯形ABCD中，AB∥CD，E，F是线段AB上的两点，且DE⊥AB，CF⊥AB，AB＝12，AD＝5，BC＝4，DE＝4，现将△ADE，△CFB分别沿DE，CF折起，使A，B两点重合于点G，得到多面体CDEFG.

(1)求证：平面DEG⊥平面CFG；

(2)求多面体CDEFG的体积．

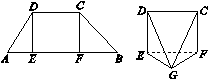
图1－7

Answer 1

解：(1)证明：因为DE⊥EF，CF⊥EF，所以四边形CDEF为矩形，

由GD＝5，DE＝4，得GE＝＝3.

由GC＝4，CF＝4，得FG＝＝4，所以EF＝5.

在△EFG中，有EF²＝GE²＋FG²，所以EG⊥GF，

又因为CF⊥EF，CF⊥FG，得，CF⊥平面EFG，

所以CF⊥EG，所以EG⊥平面CFG，即平面DEG⊥平面CFG.

(2)如图，在平面EGF中，过点G作GH⊥EF于点H，则GH＝＝.

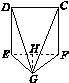
因为平面CDEF⊥平面EFG，得GH⊥平面CDEF，

V_CDEFG＝S_CDEF·GH＝16.