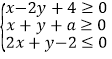题目内容
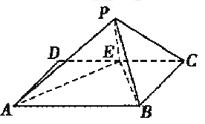
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形,![]() 底面
底面![]() ,
,![]() 是棱
是棱![]() 的中点,且
的中点,且![]() ,
,![]() .
.

(1)求证:![]() 平面
平面![]() .
.
(2)求二面角![]() 的大小;
的大小;
(3)如果![]() 是棱
是棱![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)连结![]() ,由已知数据和勾股定理可得
,由已知数据和勾股定理可得![]() ,可得
,可得![]() ,再由线面垂直关系可得
,再由线面垂直关系可得![]() 平面
平面![]() ;
;
(2)如图建立空间直角坐标系,由数量积和垂直关系可得平面![]() 的法向量
的法向量![]() ,又可得
,又可得![]() 是平面
是平面![]() 的一个法向量,求解
的一个法向量,求解![]() ,可得二面角
,可得二面角![]() 的大小;
的大小;
(3)由![]() 是棱
是棱![]() 的中点,可设
的中点,可设![]() ,
,![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,由
,由![]() ,求解可得答案.
,求解可得答案.
(1)证明:连结![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
又![]() 底面
底面![]() ,
,![]() ,
,
![]() ,
,
![]() 平面
平面![]() ;
;
(2)如图建立空间直角坐标系,
则![]() ,
,
![]() 是棱
是棱![]() 的中点,
的中点,![]() ,
,
![]()
![]() ,
,![]() .
.
设![]() 为平面
为平面![]() 的法向量,
的法向量,
![]()
 ,即
,即![]() ,
,
令![]() ,则
,则 ,
,
![]() 平面
平面![]() 的法向量
的法向量![]()
![]() 平面
平面![]() ,
,
![]()
![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
 ,
,
![]() 二面角
二面角![]() 为锐二面角,
为锐二面角,
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.
(3)解:![]() 是棱
是棱![]() 的中点,
的中点,
![]() 设
设![]() ,
,![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
![]() 由
由 .
.
![]() 直线
直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
【题目】某初级中学共有学生2000名,各年级男生女生人数如表: 已知在全校学生中随机抽取1名,抽到的是初二年级女生的概率是0.19.
初一年级 | 初二年级 | 初三年级 | |
女生 | 373 | x | y |
男生 | 377 | 370 | z |
(1)求x的值.
(2)现用分层抽样法在全校抽取48名学生,问应在初三年级学生中抽取多少名?
(3)已知y≥245,z≥245,求初三年级女生比男生多的概率.