题目内容
1.设a>0,解关于x的不等式0<$\frac{ax}{x-1}$<2.分析 先由$\frac{ax}{x-1}$>0可得x>1或x<0;$\frac{ax}{x-1}$<2,可得$\frac{(a-2)x+2}{x-1}$<0,即[(a-2)x+2][x-1]<0.分(1)当a=2时、(2)当a>2时、(3)当0<a<2时三种情况,分别求得不等式的解集,综合可得结论.
解答 解:由a>0,$\frac{ax}{x-1}$>0可得x>1或x<0;
∵$\frac{ax}{x-1}$<2,∴$\frac{(a-2)x+2}{x-1}$<0,
即[(a-2)x+2][x-1]<0.
讨论:(1)当a=2时,解得x<1.
(2)当a>2时,解得-$\frac{2}{a-2}$<x<1.
(3)当0<a<2时,x>$\frac{2}{2-a}$,或x<1.
综上可得,当a=2时,解集为{x|x<0};
当a>2时,解集为{x|-$\frac{2}{a-2}$<x<0};
当0<a<2时,解集为{x|x>$\frac{2}{2-a}$或x<0}.
点评 本题主要考查分式不等式、一元二次不等式的解法,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
12.下列命题正确的是( )
| A. | 三条两两相交的直线一定在同一平面内 | |
| B. | 垂直于同一条直线的两条直线一定平行 | |
| C. | α,β,γ是三个不同的平面,若α⊥γ,β⊥γ,则α∥β | |
| D. | m,n是平面α内的两条相交直线,l1,l2是平面β内的两条相交直线,若m∥l1,n∥l2,则α∥β |
13.若集合A={x|x2+2ax+1=0}的子集只有一个,则a的集合( )
| A. | {-1,1} | B. | {a|-1<a<1} | C. | {a|-1≤a≤1} | D. | {a|<-1或a>1} |
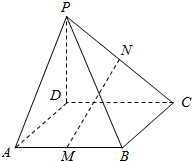 如图,在四棱锥P-ABCD中,M、N分别是AB、PC的中点.若ABCD是平行四边形.
如图,在四棱锥P-ABCD中,M、N分别是AB、PC的中点.若ABCD是平行四边形.