题目内容
在二面角α-l-β中，A∈l，B∈l，AC?α，BD?β，且AC⊥l，BD⊥l，已知AB=1，AC=BD=2，CD=
，则二面角α-l-β的余弦值为
．
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
分析：根据题意画出图形，并作出二面角的平面角，即可得出答案．
解答：解：根据题意画出图形：
在平面β内，过A作AE∥BD，过点D作DE∥l，交AE于点E．连接CE．
∵BD⊥l，∴AE⊥l．∴ED⊥平面CAE．
又AC⊥l，∴∠CAE是二面角α-l-β的平面角．
由矩形ABDE得EA=2，ED=1．
在Rt△CED中，由勾股定理得CE=
=2．
∴△ACE是等边三角形，∴∠CAE=60°，∴cos∠CAE=
．
故答案为
．
在平面β内，过A作AE∥BD，过点D作DE∥l，交AE于点E．连接CE．∵BD⊥l，∴AE⊥l．∴ED⊥平面CAE．
又AC⊥l，∴∠CAE是二面角α-l-β的平面角．
由矩形ABDE得EA=2，ED=1．
在Rt△CED中，由勾股定理得CE=
| CD2-ED2 |
∴△ACE是等边三角形，∴∠CAE=60°，∴cos∠CAE=
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
点评：由二面角的定义正确作出其平面角是解题的关键．
练习册系列答案
相关题目
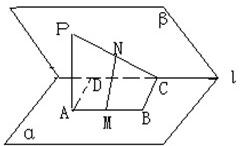如图：在二面角α-l-β中，A、B∈α，C、D∈l，ABCD为矩形，p∈β，PA⊥α，且PA=AD，M、N依次是AB、PC的中点，