题目内容
在二面角α-l-β中，点A∈α，AC⊥l，C为垂足，点B∈β，BD⊥l，D为垂足，若AB=AC=2，BD=CD=1，则二面角α-l-β的大小等于（ ）[
分析：先作出二面角的平面角，再在三角形中，即可求得面面角．
解答：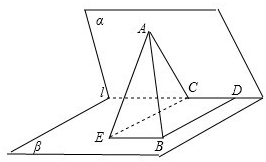
解：由题意，过C在β内作EC⊥l，垂足为C，截取EC=BD=1，则∠ACE为二面角α-l-β的平面角
在直角△ABE中，AB=2，BE=1，则AE=
在△AEC中，AC=2，CE=1，AE=
，∴∠AEC=90°
∴∠ACE=60°
故选C．
解：由题意，过C在β内作EC⊥l，垂足为C，截取EC=BD=1，则∠ACE为二面角α-l-β的平面角在直角△ABE中，AB=2，BE=1，则AE=
| 3 |
在△AEC中，AC=2，CE=1，AE=
| 3 |
∴∠ACE=60°
故选C．
点评：本题考查面面角，考查学生的计算能力，解题的关键是正确作出面面角，属于中档题．
练习册系列答案
相关题目
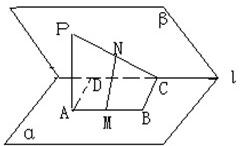如图：在二面角α-l-β中，A、B∈α，C、D∈l，ABCD为矩形，p∈β，PA⊥α，且PA=AD，M、N依次是AB、PC的中点，