题目内容
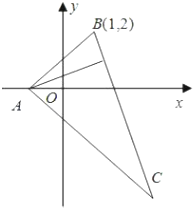 在△ABC中,已知BC边上的高所在直线的方程为x-2y+1=0,∠A平分线所在直线的方程为y=0,若点B的坐标为(1,2),
在△ABC中,已知BC边上的高所在直线的方程为x-2y+1=0,∠A平分线所在直线的方程为y=0,若点B的坐标为(1,2),(Ⅰ)求直线BC的方程;
(Ⅱ)求点C的坐标.
分析:(I)根据垂直的位置关系,算出直线BC的斜率为-2,利用直线方程的点斜式列式,化简整理即可得到直线BC的方程;
(II)由BC边的高所在直线方程和y=0,解出A(-1,0),从而得出直线AB的方程.由直线AC、AB关于直线y=0对称,算出AC方程,最后将AC方程与BC方程联解,即可得出点C的坐标.
(II)由BC边的高所在直线方程和y=0,解出A(-1,0),从而得出直线AB的方程.由直线AC、AB关于直线y=0对称,算出AC方程,最后将AC方程与BC方程联解,即可得出点C的坐标.
解答:解:(Ⅰ)设BC边上的高为AD,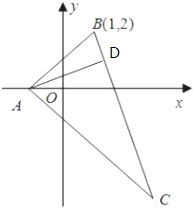
∵BC与AD互相垂直,且AD的斜率为
,
∴直线BC的斜率为k=
=-2,
结合B(1,2),可得BC的点斜式方程:y-2=-2(x-1),
化简整理,得 2x+y-4=0,即为所求的直线BC方程.
(Ⅱ)由x-2y+1=0和y=0联解,得A(-1,0)
由此可得直线AB方程为:
=
,即y=x+1
∵AB,AC关于角A平分线x轴对称,
∴直线AC的方程为:y=-x-1
∵直线BC方程为y=-2x+4
∴将AC、BC方程联解,得x=5,y=-6
因此,可得C点的坐标为(5,-6).

∵BC与AD互相垂直,且AD的斜率为
| 1 |
| 2 |
∴直线BC的斜率为k=
| -1 | ||
|
结合B(1,2),可得BC的点斜式方程:y-2=-2(x-1),
化简整理,得 2x+y-4=0,即为所求的直线BC方程.
(Ⅱ)由x-2y+1=0和y=0联解,得A(-1,0)
由此可得直线AB方程为:
| y-0 |
| 2-0 |
| x+1 |
| 1+1 |
∵AB,AC关于角A平分线x轴对称,
∴直线AC的方程为:y=-x-1
∵直线BC方程为y=-2x+4
∴将AC、BC方程联解,得x=5,y=-6
因此,可得C点的坐标为(5,-6).
点评:本题给出三角形的角平分线和高所在直线方程,求边BC所在直线的方程和点C坐标.着重考查了直线的基本量与基本形式、直线的位置关系等知识,属于基础题.

练习册系列答案
相关题目
 在△ABC中,已知B=45°,D是BC上一点,AD=5,AC=7,DC=3,求AB的长.
在△ABC中,已知B=45°,D是BC上一点,AD=5,AC=7,DC=3,求AB的长. 如图,在△ABC中,已知B=
如图,在△ABC中,已知B=