Question

已知直线l的方程为x=-2，且直线l与x轴交于点M，圆O：x²+y²=1 与x轴交于A，B两点．
（1）求以l为准线，中心在原点，且与圆O恰有两个公共点的椭圆方程；
（2）过M点作直线l₁与圆相切于点N，设（2）中椭圆的两个焦点分别为F₁F₂，求三角形△NF₁F₂面积．

Answer 1

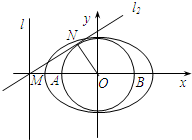解：（1）设椭圆方程为，半焦距为c，则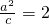
∵椭圆与圆O恰有两个不同的公共点，根据椭圆与圆的对称性，
则a=1或b=1
当a=1时，c=，b²=a²-c²=，
∴所求椭圆方程为；
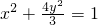当b=1时，b²+c²=2c，∴c=1，∴a²=b²+c²=2
∴所求椭圆方程为；
（2）设切点为N，则由题意得，在Rt△MON中，MO=2，ON=1，则∠NMO=30°，
N点的坐标为，
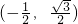若椭圆为，其焦点F₁，F₂分别为A（-1，0），B（1，0），
故=，
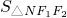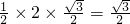若椭圆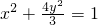为，其焦点为，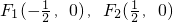
此时=．
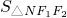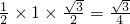分析：（1）由题意设出焦点在x轴上的椭圆的标准方程，根据椭圆经过y轴上的点（0，1），分长半轴等于1和短半轴等于1两种情况求解椭圆的标准方程；
（2）由平面几何知识求出点N的坐标，求出两个椭圆的焦点坐标，直接利用三角形的面积公式求三角形△NF₁F₂面积．
点评：本题考查了椭圆的简单几何性质，考查了圆与圆锥曲线的综合，考查了分类讨论的数学思想方法，属中档题．