题目内容
条件甲:“f'(x)=2ax+b或
”;条件乙:“a=
,b=2n对x∈R恒成立”,则要使甲是乙的充要条件,命题甲的条件中须删除的一部分是
|
| 1 |
| 2 |
f′(x)=2ax+b
f′(x)=2ax+b
.分析:根据充要条件的定义条件甲和条件乙,可以互推,从而进行求解;
解答:解:∵条件甲:“f'(x)=2ax+b或
”;条件乙:“a=
,b=2n对x∈R恒成立”,
∵16n2a=4nb,⇒4na=b,⇒a=
=
=
,
∴条件甲⇒条件乙,
若条件乙:“a=
,b=2n对x∈R恒成立,
推不出f′(x)=2ax+b,可以推出b=2n,16n2a=4nb,
∴命题甲的条件中须删除的一部分是f′(x)=2ax+b,
故答案为:f′(x)=2ax+b;
|
| 1 |
| 2 |
∵16n2a=4nb,⇒4na=b,⇒a=
| b |
| 4n |
| b |
| 2×2n |
| 1 |
| 2 |
∴条件甲⇒条件乙,
若条件乙:“a=
| 1 |
| 2 |
推不出f′(x)=2ax+b,可以推出b=2n,16n2a=4nb,
∴命题甲的条件中须删除的一部分是f′(x)=2ax+b,
故答案为:f′(x)=2ax+b;
点评:此题出的比较新颖,主要考查了必要条件、充分条件与充要条件的判断,属于基础题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
命题甲:f(x)是 R上的单调递增函数;命题乙:?x1<x2,f(x1)<f(x2).则甲是乙的( )
| A、充分不必要条件 | B、必要不充分条件 | C、充分且必要条件 | D、既不充分也不必要条件 |
 ”;条件乙:“
”;条件乙:“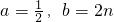 对x∈R恒成立”,则要使甲是乙的充要条件,命题甲的条件中须删除的一部分是________.
对x∈R恒成立”,则要使甲是乙的充要条件,命题甲的条件中须删除的一部分是________. ”;条件乙:“
”;条件乙:“ 对x∈R恒成立”,则要使甲是乙的充要条件,命题甲的条件中须删除的一部分是 .
对x∈R恒成立”,则要使甲是乙的充要条件,命题甲的条件中须删除的一部分是 .