题目内容
有以下真命题:设an1,an2,…,anm是公差为d的等差数列{an}中的任意m个项,若
=p+
(0≤r<m,p、r、m∈N或r=0)①,则有
=ap+
d②,特别地,当r=0时,称ap为an1,an2,…,anm的等差平均项.
(1)当m=2,r=0时,试写出与上述命题中的(1),(2)两式相对应的等式;
(2)已知等差数列{an}的通项公式为an=2n,试根据上述命题求a1,a3,a10,a18的等差平均项;
(3)试将上述真命题推广到各项为正实数的等比数列中,写出相应的真命题.
| n1+n2+…+nm |
| m |
| r |
| m |
| an1+an2+…+anm |
| m |
| r |
| m |
(1)当m=2,r=0时,试写出与上述命题中的(1),(2)两式相对应的等式;
(2)已知等差数列{an}的通项公式为an=2n,试根据上述命题求a1,a3,a10,a18的等差平均项;
(3)试将上述真命题推广到各项为正实数的等比数列中,写出相应的真命题.
分析:(1)当m=2,r=0时,
=p+
,可化为
=p,
=ap+
d可化为
=ap;
(2)由等差数列{an}的通项公式为an=2n,可得a1,a3,a10,a18的值,代入公式可得a1,a3,a10,a18的等差平均项;
(3)根据等比数列运算级比等差数列高的一般性质规律,可以类比推断出设an1,an2,…,anm是公比为q的等比数列{an}中的任意m个项,若
=p+
(0≤r<m,p、r、m∈N或r=0①,则有 m
=apq
②,特别地,当r=0时,称ap为an1,an2,…,anm的等比平均项.
| n1+n2+…+nm |
| m |
| r |
| m |
| n1+n2 |
| 2 |
| an1+an2+…+anm |
| m |
| r |
| m |
| an1+an2 |
| 2 |
(2)由等差数列{an}的通项公式为an=2n,可得a1,a3,a10,a18的值,代入公式可得a1,a3,a10,a18的等差平均项;
(3)根据等比数列运算级比等差数列高的一般性质规律,可以类比推断出设an1,an2,…,anm是公比为q的等比数列{an}中的任意m个项,若
| n1+n2+…+nm |
| m |
| r |
| m |
| an1an2…anm |
| r |
| m |
解答:解:(1)∵若
=p+
(0≤r<m,p、r、m∈N或r=0)①,
则有
=ap+
d②,
又∵当m=2,r=0时,
=p+
,可化为
=p,
=ap+
d可化为
=ap;
故原命题可化为:若
=p,则
=ap.
(2)∵an=2n,
∴a1=2,a3=6,a10=20,a18=36.
∵
=8,
∴
=a8=16.
(3)由设an1,an2,…,anm是公差为d的等差数列{an}中的任意m个项,
若
=p+
(0≤r<m,p、r、m∈N或r=0)①,
则有
=ap+
d②,
特别地,当r=0时,称ap为an1,an2,…,anm的等差平均项.
根据等比数列运算级比等差数列高的一般性质规律,可以类比推断出以下真命题:
设an1,an2,…,anm是公比为q的等比数列{an}中的任意m个项,
若
=p+
(0≤r<m,p、r、m∈N或r=0①,
则有 m
=apq
②,
特别地,当r=0时,称ap为an1,an2,…,anm的等比平均项.
| n1+n2+…+nm |
| m |
| r |
| m |
则有
| an1+an2+…+anm |
| m |
| r |
| m |
又∵当m=2,r=0时,
| n1+n2+…+nm |
| m |
| r |
| m |
| n1+n2 |
| 2 |
| an1+an2+…+anm |
| m |
| r |
| m |
| an1+an2 |
| 2 |
故原命题可化为:若
| n1+n2 |
| 2 |
| an1+an2 |
| 2 |
(2)∵an=2n,
∴a1=2,a3=6,a10=20,a18=36.
∵
| 1+3+10+18 |
| 4 |
∴
| a1+a3+a10+a18 |
| 4 |
(3)由设an1,an2,…,anm是公差为d的等差数列{an}中的任意m个项,
若
| n1+n2+…+nm |
| m |
| r |
| m |
则有
| an1+an2+…+anm |
| m |
| r |
| m |
特别地,当r=0时,称ap为an1,an2,…,anm的等差平均项.
根据等比数列运算级比等差数列高的一般性质规律,可以类比推断出以下真命题:
设an1,an2,…,anm是公比为q的等比数列{an}中的任意m个项,
若
| n1+n2+…+nm |
| m |
| r |
| m |
则有 m
| an1an2…anm |
| r |
| m |
特别地,当r=0时,称ap为an1,an2,…,anm的等比平均项.
点评:本题考查的知识点是类比推理,等差数列的性质,其中正确理解新定义等差平均项的含义,及等差数列到等比数列的类比法则是解答本题的关键.

练习册系列答案
相关题目
 ,
,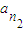 ,…,
,…,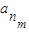 是公差为d的等差数列{an}中的任意m个项,若
是公差为d的等差数列{an}中的任意m个项,若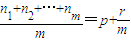 (0≤r<m,p、r、m∈N或r=0)①,则有
(0≤r<m,p、r、m∈N或r=0)①,则有 ②,特别地,当r=0时,称ap为
②,特别地,当r=0时,称ap为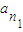 ,
,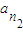 ,…,
,…,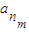 的等差平均项.
的等差平均项.