题目内容
叙述并证明正弦定理.
 ,运用向量法表示来证明,或者借助于三角函数的性质来证明。
,运用向量法表示来证明,或者借助于三角函数的性质来证明。
解析试题分析:
证明(向量法):
(1)当 为直角三角形时,
为直角三角形时, .
.
由锐角三角函数的定义,有 ,所以
,所以 .
.
又 ,所以
,所以 .
.
(2)当 为锐角三角形时,如图示
为锐角三角形时,如图示
过点 作单位向量
作单位向量 垂直于
垂直于 ,则
,则 ,
, .
.
又由图知, ,为了与图中有关的三角函数建立联系,对上面向量等式的两边同取与向量
,为了与图中有关的三角函数建立联系,对上面向量等式的两边同取与向量 的数量积运算,得到:
的数量积运算,得到: ,所以
,所以 ,即
,即
所以 .
.
同理,过点 作与
作与 垂直的单位向量
垂直的单位向量 ,可得
,可得 .所以
.所以 .
.
(2)当 为钝角三角形时,不妨设
为钝角三角形时,不妨设 ,如图示
,如图示
过点 作与
作与 垂直的单位向量
垂直的单位向量 ,
, ,
, .
.
同样,可证得 .因此,对于任意三角形均有
.因此,对于任意三角形均有 .
.
注:还可运用三角函数定义法证明或者等面积法证明。
考点:正弦定理
点评:掌握运用向量的方法来证明正弦定理,简单明了,感受向量的几何运用,属于基础题。

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目

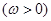 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减;如图,四边形
上单调递减;如图,四边形 中,
中, ,
, ,
, 为
为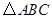 的内角
的内角 的对边,
的对边, .
.
 ;
; ,设
,设 ,
, ,
, ,求四边形
,求四边形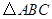 中,内角
中,内角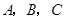 对边的边长分别是
对边的边长分别是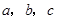 ,已知
,已知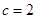 ,
, .
.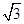 ,求
,求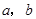 ;
;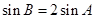 ,求
,求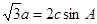
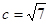 ,且△ABC的面积为
,且△ABC的面积为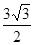 ,求a+b的值。
,求a+b的值。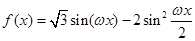 (
(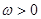 )的最小正周期为
)的最小正周期为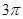 ,
,  时,求函数
时,求函数 的最小值;
的最小值;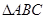 中,若
中,若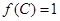 ,且
,且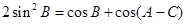 ,求
,求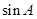 的值。
的值。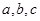 分别为
分别为 三个内角
三个内角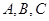 的对边,且
的对边,且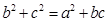 .
.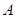 的大小;
的大小;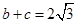 ,
,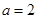 ,求
,求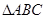 的面积.
的面积.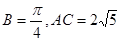 ,
,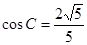 .
.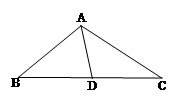
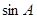 ;
;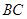 的中点为
的中点为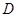 ,求中线
,求中线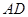 的长.
的长. 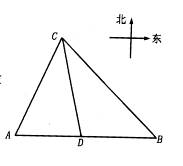
 的内角
的内角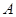 、
、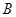 、
、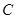 的对边分别为
的对边分别为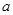 、
、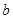 、
、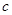 ,已知
,已知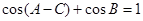 ,
,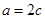 ,求
,求